ЬтФПФкШн
ШчЭМЃЌЕШбќжБНЧШ§НЧаЮжНЦЌABCжаЃЌAC=BC=4ЃЌЁЯACB=90ЁуЃЌжБНЧБпACдкxжсЩЯЃЌBЕудкЕкЖўЯѓЯоЃЌAЃЈ1ЃЌ0ЃЉЃЌABНЛyжсгкEЃЌНЋжНЦЌЙ§EЕуелЕўЪЙBEгыEAЫљдкжБЯпжиКЯЃЌЕУЕНелКлEFЃЈFдкxжсЩЯЃЉЃЌдйеЙПЊЛЙдбиEFМєПЊЕУЕНЫФБпаЮBCFEЃЌШЛКѓАбЫФБпаЮBCFEДгEЕуПЊЪМбиЩфЯпEAЦНвЦЃЌжСBЕуЕНДяAЕуЭЃжЙЃЎЩшЦНвЦЪБМфЮЊtЃЈsЃЉЃЌвЦЖЏЫйЖШЮЊУПУы1Иі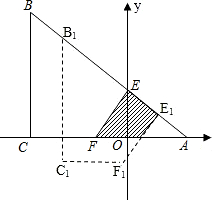 ЕЅЮЛГЄЖШЃЌЦНвЦжаЫФБпаЮBCFEгыЁїAEFжиЕўЕФУцЛ§ЮЊSЃЎ
ЕЅЮЛГЄЖШЃЌЦНвЦжаЫФБпаЮBCFEгыЁїAEFжиЕўЕФУцЛ§ЮЊSЃЎ
ЃЈ1ЃЉЧѓелКлEFЕФГЄЃЛ
ЃЈ2ЃЉЪЧЗёДцдкФГвЛЪБПЬtЪЙЦНвЦжажБНЧЖЅЕуCОЙ§ХзЮяЯпy=x2+4x+3ЕФЖЅЕуЃПШєДцдкЃЌЧѓГіtжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉжБНгаДГіSгыtЕФКЏЪ§ЙиЯЕЪНМАздБфСПtЕФШЁжЕЗЖЮЇЃЎ
 ЕЅЮЛГЄЖШЃЌЦНвЦжаЫФБпаЮBCFEгыЁїAEFжиЕўЕФУцЛ§ЮЊSЃЎ
ЕЅЮЛГЄЖШЃЌЦНвЦжаЫФБпаЮBCFEгыЁїAEFжиЕўЕФУцЛ§ЮЊSЃЎЃЈ1ЃЉЧѓелКлEFЕФГЄЃЛ
ЃЈ2ЃЉЪЧЗёДцдкФГвЛЪБПЬtЪЙЦНвЦжажБНЧЖЅЕуCОЙ§ХзЮяЯпy=x2+4x+3ЕФЖЅЕуЃПШєДцдкЃЌЧѓГіtжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉжБНгаДГіSгыtЕФКЏЪ§ЙиЯЕЪНМАздБфСПtЕФШЁжЕЗЖЮЇЃЎ
ЃЈ1ЃЉЁпелЕўКѓBEгыEAЫљдкжБЯпжиКЯ
ЁрFEЁЭEAгжRtЁїABCжаAC=BC
ЁрЁЯCAB=45Ёу
ЁрEF=EA
ЁпAЃЈ1ЃЌ0ЃЉ
ЁрOA=OE=1ЃЌAE=
ЁрелКлEF=
ЃЎ
ЃЈ2ЃЉДцдкЃЌЩшCPЁЮBAНЛYжсгкPЃЌ
дђЁїPOCЮЊЕШбќжБНЧШ§НЧаЮЃЌжБНЧЖЅЕуCдкЩфЯпCPЩЯвЦЖЏ
ЁпAC=4ЃЌOA=1
ЁрOC=OP=3
ЁрCЃЈ-3ЃЌ0ЃЉЃЌPЃЈ0ЃЌ-3ЃЉПЩЧѓЕУPCЫљдкжБЯпНтЮіЪНЮЊЃКy=-x-3
ЁпжБНЧЖЅЕуCДгЃЈ-3ЃЌ0ЃЉЮЛжУвЦЖЏЕНЃЈ-2ЃЌ-1ЃЉЪБЃЌЫЎЦНвЦЖЏОрРыЮЊ|-2-ЃЈ-3ЃЉ|=1ЃЈГЄЖШЕЅЮЛЃЉ
ЁржБНЧЖЅЕуCДгПЊЪМЕНОЙ§ДЫХзЮяЯпЖЅЕувЦЖЏЕФЪБМфt=
=
(s)ЃЎ
ЃЈ3ЃЉЕБ0ЁмtЁм
ЪБЃЌ
ЫФБпаЮBCFEгыЁїAEFжиЕўЕФУцЛ§ЮЊЃКжБНЧЬнаЮEFQE 1ЃЌ
ЙЪУцЛ§ЮЊЃКS=
ЃЈEF+E1QЃЉЁСEE1=
tЃЈ
-t+
ЃЉ=-
t2+
tЃЌ
ЭЌРэПЩЕУГіЦфЫќКЏЪ§НтЮіЪНЃК
s=
ЃЎ

ЁрFEЁЭEAгжRtЁїABCжаAC=BC
ЁрЁЯCAB=45Ёу
ЁрEF=EA
ЁпAЃЈ1ЃЌ0ЃЉ
ЁрOA=OE=1ЃЌAE=
| 2 |
ЁрелКлEF=
| 2 |
ЃЈ2ЃЉДцдкЃЌЩшCPЁЮBAНЛYжсгкPЃЌ
дђЁїPOCЮЊЕШбќжБНЧШ§НЧаЮЃЌжБНЧЖЅЕуCдкЩфЯпCPЩЯвЦЖЏ
ЁпAC=4ЃЌOA=1
ЁрOC=OP=3
ЁрCЃЈ-3ЃЌ0ЃЉЃЌPЃЈ0ЃЌ-3ЃЉПЩЧѓЕУPCЫљдкжБЯпНтЮіЪНЮЊЃКy=-x-3
ЁпжБНЧЖЅЕуCДгЃЈ-3ЃЌ0ЃЉЮЛжУвЦЖЏЕНЃЈ-2ЃЌ-1ЃЉЪБЃЌЫЎЦНвЦЖЏОрРыЮЊ|-2-ЃЈ-3ЃЉ|=1ЃЈГЄЖШЕЅЮЛЃЉ
ЁржБНЧЖЅЕуCДгПЊЪМЕНОЙ§ДЫХзЮяЯпЖЅЕувЦЖЏЕФЪБМфt=
| 1 | ||||
|
| 2 |

ЃЈ3ЃЉЕБ0ЁмtЁм
| 2 |
ЫФБпаЮBCFEгыЁїAEFжиЕўЕФУцЛ§ЮЊЃКжБНЧЬнаЮEFQE 1ЃЌ
ЙЪУцЛ§ЮЊЃКS=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
ЭЌРэПЩЕУГіЦфЫќКЏЪ§НтЮіЪНЃК
s=
|


СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП
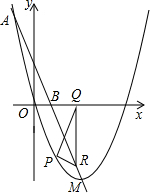


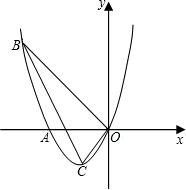
 ЕуCЕФКсзјБъЮЊ1ЃЌ
ЕуCЕФКсзјБъЮЊ1ЃЌ