题目内容
如图，⊙O1和⊙O2相交于点A、B，且⊙O2的圆心O2在圆⊙O1的圆上，P是⊙O2上一点，已知∠AO1B=60°，那么∠APB的度数是
- A.60°
- B.65°
- C.70°
- D.75°
D
分析：连接AO2、BO2，设点E是优弧上的一点，由圆周角定理可求，∠E=
∠AO1B=30°，由圆内接四边形的对角互补，可求∠AO2B=180°-∠E=150°，∠P=∠AO2B=75°．
解答：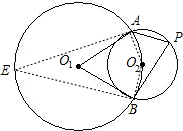
解：连接AO2、BO2，
设点E是优弧上的一点，
∴∠E=∠AO1B=30°，
∴∠AO2B=180°-∠E=150°，
∠P=∠AO2B=75°．
故选D．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．和圆内接四边形对角互补的知识．
分析：连接AO2、BO2，设点E是优弧上的一点，由圆周角定理可求，∠E=
∠AO1B=30°，由圆内接四边形的对角互补，可求∠AO2B=180°-∠E=150°，∠P=∠AO2B=75°．解答：
解：连接AO2、BO2，设点E是优弧上的一点，
∴∠E=
∠AO1B=30°，∴∠AO2B=180°-∠E=150°，
∠P=
∠AO2B=75°．故选D．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．和圆内接四边形对角互补的知识．
练习册系列答案
相关题目
20、已知：如图，⊙O1和⊙O2相交于A、B两点，动点P在⊙O2上，且在⊙1外，直线PA、PB分别交⊙O1于C、D，问：⊙O1的弦CD的长是否随点P的运动而发生变化？如果发生变化，请你确定CD最长和最短时P的位置，如果不发生变化，请你给出证明．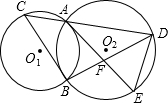
长⊙O1相交于C点，连接BC，过A点作AE∥BC与⊙O相交于E点，与BD相交于F点．
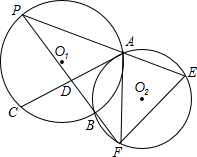、PB的延长线分别交⊙O2于点E、F，PB交AC于D．
16、如图．⊙O1和⊙O2外切于点A，BC是⊙O1和⊙O2的公切线，B、C为切点，求证：AB⊥AC．
（2001•黄冈）已知，如图，⊙O1和⊙O2内切于点P，过点P的直线交⊙O1于点D，交⊙O2于点E；DA与⊙O2相切，切点为C．