Question

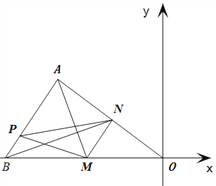
【题目】如图，在平面直角坐标系中，△AOB的三个顶点的坐标分别是A(-4,3)，B(-6,0)， O是原点．点M是OB边上异于O，B的一动点，过点M作MN//AB，点P是AB边上的任意点，连接AM，PM，PN，BN．设点.

（1）求出OA所在直线的解析式，并求出点M的坐标为(-1,0)时，点N的坐标．

（2）若 = 时，求此时点N的坐标．

Answer 1

【答案】（1）；N（， ）；（2）N（，2）

【解析】试题分析：（1）设y=kx（k≠0），将点A的坐标代入解析式求出k的值，写出解析式；（2）因为MN//AB，所以N点的横坐标与A点的横坐标之比为，又因为A的坐标已知，故可求出N点的横坐标，将N点的横坐标代入直线OA的解析式，即可求出N的纵坐标；（3）因为MN//AB，根据平行线间的距离相等，所以S△PMN=S△BMN，S△ANB=S△ABM，所以将转化为，已知hA，不难求出hN，将点N的坐标代入直线OA解析式即可求出N纵坐标.

试题解析：

解：（1）由于A(－4,3)，设直线OA为y=kx（k≠0），得y=－x；

又因OA=5，OB=6，OM=1，且MN//AB，

所以N点的横坐标与A点的横坐标之比为，

即点N的横坐标为－，代入y=－x得，N（－， ）；

（2）∵MN//AB，根据平行线间的距离相等，

∴S△PMN=S△BMN，S△ANB=S△ABM，

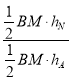∴===（其中、为A、N点的纵坐标），

∴，

又∵A(－4,3)，

∴hN=2，即yN=2，

将yN=2代入y=－x，得x=－，

∴N(－，2).