题目内容
如图(1),四边形ABCD和BEFC都是平行四边形,其中,A、B、E在一条直线上.已知AD=6,AB=BE=2,∠E=![]() .
.
如图(2),将四边形ABCD沿直线l平移,移动后,形成四边形AEFD.
1)在平移过程中,四边形AEFD是否可以为矩形?如果可以,请直接写出矩形的面积;如果不可以,请说明理由;
(2)试探究:如何平移,可以使得四边形AEFD为菱形?(借助备用图,写出具体过程和结论)


(1)12![]() cm2; ……………………(2分)
cm2; ……………………(2分)
(2)①如图,若四边形ABCD沿直线l向右平移形成菱形,过点A做AP⊥直线l,
∵∠AB′P=60,∴∠B′AP=30.∵AB=2,∴B′P=![]() A B′=1.
A B′=1.
在Rt△AB′P中,根据勾股定理,得 AP2= AB′2-B′P2, ∴AP=![]() .
.
∵四边形AEFD为菱形,∴AE=AD=6.
 根据题意有A B′∥EB,∴∠EBQ=∠A B′Q.
根据题意有A B′∥EB,∴∠EBQ=∠A B′Q.
在△A B′Q和△EB![]() Q中,
Q中,
![]() ∠A B′Q =∠EBQ,
∠A B′Q =∠EBQ,
∠AQ B′=∠EQB,
AB′=EB,
 .
.
 ∵四边形AEFD为菱形,∴AE=AD=6.
∵四边形AEFD为菱形,∴AE=AD=6.
根据题意有A B′∥EB,∴∠EBQ=∠A B′Q .
在△A B′Q和△EBQ中,
![]() ∠A B′Q =∠EBQ,
∠A B′Q =∠EBQ,
∠AQ B′=∠EQB![]() ,
,
AB′=EB,
∴△A B′Q≌△EBQ.
∴AQ=![]() AE=3,BQ= B′Q=
AE=3,BQ= B′Q=![]() BB′.
BB′.
在Rt△AQP中,根据勾股定理,得 QP2= AQ2- AP2
∴QP=![]() .
.
∵B′Q= QP+B′P=![]() +1,
+1,
∴BB′=2![]() +2,即四边形ABCD沿直线l向左平移(2
+2,即四边形ABCD沿直线l向左平移(2![]() +2)cm可以得到菱形AEFD.
+2)cm可以得到菱形AEFD.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
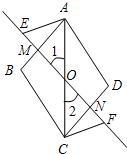 56、如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.
56、如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF. 18、如图,已知平行四边形ABCD.
18、如图,已知平行四边形ABCD.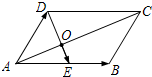 如图,已知平行四边形ABCD,E是边AB的中点,连接AC、DE交于点O.记向量
如图,已知平行四边形ABCD,E是边AB的中点,连接AC、DE交于点O.记向量
 画出如图所示的平行四边形ABCD绕点D顺时针旋转90°后的图形,再经几次90°旋转可以与原来图形重合.
画出如图所示的平行四边形ABCD绕点D顺时针旋转90°后的图形,再经几次90°旋转可以与原来图形重合.