题目内容
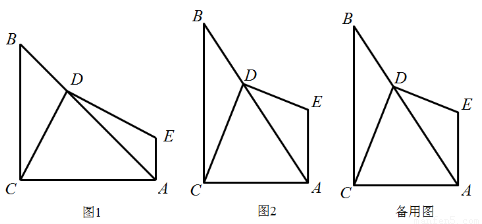
 如图,AB∥DE,那么∠BCD=
如图,AB∥DE,那么∠BCD=
- A.∠2-∠1
- B.∠1+∠2
- C.180°+∠1-∠2
- D.180°+∠2-2∠1
C
分析:过点C作CF∥AB,由AB∥DE可知,AB∥DE∥CF,再由平行线的性质可知,∠1=∠BCF,∠2+∠DCF=180°,故可得出结论.
解答: 解:过点C作CF∥AB,
解:过点C作CF∥AB,
∵AB∥DE,
∴AB∥DE∥CF,
∴∠BCF=∠1①,∠2+∠DCF=180°②,
∴①+②得,∠BCF+∠DCF+∠2=∠1+180°,即∠BCD=180°+∠1-∠2.
故选C.
点评:本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.
分析:过点C作CF∥AB,由AB∥DE可知,AB∥DE∥CF,再由平行线的性质可知,∠1=∠BCF,∠2+∠DCF=180°,故可得出结论.
解答:
 解:过点C作CF∥AB,
解:过点C作CF∥AB,∵AB∥DE,
∴AB∥DE∥CF,
∴∠BCF=∠1①,∠2+∠DCF=180°②,
∴①+②得,∠BCF+∠DCF+∠2=∠1+180°,即∠BCD=180°+∠1-∠2.
故选C.
点评:本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.

练习册系列答案
相关题目