题目内容
△ABC的三条边长之比为：2：5：6，与其相似的△A′B′C′的最大边长为15cm，那么它的最小边长为________，另一边长为________．
5cm 
cm
分析：根据相似三角形对应边成比例，列出比例式进行计算即可．
解答：设△A′B′C′的最小边是xcm，另一边是ycm，
∵△ABC∽△A′B′C′，
∴
=
，
=
，
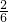解得x=5，y=．
故答案为：5cm，cm．
点评：本题考查了相似三角形对应边成比例的性质，是基础题，找准对应边列出比例式计算即可．
cm分析：根据相似三角形对应边成比例，列出比例式进行计算即可．
解答：设△A′B′C′的最小边是xcm，另一边是ycm，
∵△ABC∽△A′B′C′，
∴
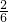=，=，解得x=5，y=
．故答案为：5cm，
cm．点评：本题考查了相似三角形对应边成比例的性质，是基础题，找准对应边列出比例式计算即可．
练习册系列答案
应用题作业本系列答案
相关题目
△ABC三条边长之比为2：5：6，与其相似的另一个△A′B′C′的最大边为15cm，那么它的最小边为（ ）
| A、5cm | B、6cm | C、7cm | D、8cm |
的最大边长为15 cm，那么它的最小边为________，另一边为________．