题目内容
【题目】阅读材料I:
教材中我们学习了:若关于![]() 的一元二次方程
的一元二次方程![]() 的两根为
的两根为![]()
![]() ,根据这一性质,我们可以求出己知方程关于
,根据这一性质,我们可以求出己知方程关于![]() 的代数式的值.
的代数式的值.
问题解决:
(1)已知![]() 为方程
为方程![]() 的两根,则:
的两根,则:![]() __ _,
__ _,![]() __ _,那么_
__ _,那么_![]() (请你完成以上的填空)
(请你完成以上的填空)
阅读材料:II
已知![]() ,且
,且![]() .求
.求![]() 的值.
的值.
解:由![]() 可知
可知![]()
![]()
![]()
又![]() 且
且![]() ,即
,即![]()
![]() 是方程
是方程![]() 的两根.
的两根.
![]()
问题解决:
(2)若![]() 且
且![]() 则
则![]() ;
;
(3)已知![]() 且
且![]() .求
.求![]() 的值.
的值.
【答案】(1)-3;-1;11;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据根与系数的关系可求出x1+x2和x1x2的值,然后利用完全平方公式将![]() 变形为
变形为![]() ,再代值求解即可;
,再代值求解即可;
(2)利用加减法结合因式分解解方程组,然后求值即可;
(3)根据材料中的的解法将等式变形,然后将m和![]() 看作一个整体,利用一元二次方程根与系数的关系,可求出m+
看作一个整体,利用一元二次方程根与系数的关系,可求出m+![]() 和m
和m![]() 的值,然后再代值求解.
的值,然后再代值求解.
解:(1)∵![]() 为方程
为方程![]() 的两根,
的两根,
∴![]() ,
,![]()
![]()
故答案为:-3;-1;11;
(2)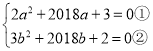
①×b得:![]()
②×a得:![]()
③-④得:![]()
![]()
![]()
![]()
![]() 或
或![]()
∴![]() 或
或![]()
又∵![]()
∴![]() ,即
,即![]()
故答案为:![]() ;
;
(3)由n2+3n-2=0可知n≠0;
∴![]()
∴![]()
又2m2-3m-1=0,且mn≠1,即m≠![]() ;
;
∴m、![]() 是方程2x2-3x-1=0的两根,
是方程2x2-3x-1=0的两根,
∴m+![]() =
=![]() ,m
,m![]() =
=![]() ;
;
∴![]() .
.

练习册系列答案
相关题目