题目内容
正方形ABCD内有一点E,且△ABE是面积为4 的正三角形,在对角线AC上有一点P,当PD+PE的值最小时,则这个最小值为________.
的正三角形,在对角线AC上有一点P,当PD+PE的值最小时,则这个最小值为________.
4
分析:根据△ABE是面积为4 的正三角形,可得BE的长,根据AC,BD是正方形ABCD的对角线,可得直线AC是线段BD的垂直平分线,再根据直线AC是线段BD的垂直平分线,可得PB=PD,可得答案.
的正三角形,可得BE的长,根据AC,BD是正方形ABCD的对角线,可得直线AC是线段BD的垂直平分线,再根据直线AC是线段BD的垂直平分线,可得PB=PD,可得答案.
解答:如图 △ABE是面积为4
△ABE是面积为4 的正三角形,
的正三角形,
 ,
,
∴BE=AB=4
.∵直线AC是线段BD的垂直平分线,
∴PB=PD.
PD+PE=PB+PE=PB=4,
故答案为:4.
点评:本题考查了轴对称-最短线路问题,线段垂直平分线上的点到线段两端点的距离相等,是解题关键.
分析:根据△ABE是面积为4
 的正三角形,可得BE的长,根据AC,BD是正方形ABCD的对角线,可得直线AC是线段BD的垂直平分线,再根据直线AC是线段BD的垂直平分线,可得PB=PD,可得答案.
的正三角形,可得BE的长,根据AC,BD是正方形ABCD的对角线,可得直线AC是线段BD的垂直平分线,再根据直线AC是线段BD的垂直平分线,可得PB=PD,可得答案.解答:如图
 △ABE是面积为4
△ABE是面积为4 的正三角形,
的正三角形, ,
,∴BE=AB=4
.∵直线AC是线段BD的垂直平分线,
∴PB=PD.
PD+PE=PB+PE=PB=4,
故答案为:4.
点评:本题考查了轴对称-最短线路问题,线段垂直平分线上的点到线段两端点的距离相等,是解题关键.

练习册系列答案
相关题目
 如图,在正方形ABCD内有一折线段,其中AE丄EF,EF丄FC,并且AE=6,EF=8,FC=10,则正方形与其外接圆之间形成的阴影部分的面积为
如图,在正方形ABCD内有一折线段,其中AE丄EF,EF丄FC,并且AE=6,EF=8,FC=10,则正方形与其外接圆之间形成的阴影部分的面积为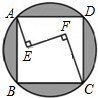 (2012•朝阳)如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=4,EF=8,FC=12,则正方形与其外接圆形成的阴影部分的面积为
(2012•朝阳)如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=4,EF=8,FC=12,则正方形与其外接圆形成的阴影部分的面积为 如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=6,EF=8,FC=10,则正方形与其外接圆之间形成的每个弓形的面积为
如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=6,EF=8,FC=10,则正方形与其外接圆之间形成的每个弓形的面积为