题目内容
在平面直角坐标系中,二次函数y=ax2+c与x轴交于A、B两点,与y轴交于点C(0,4),已知点B(2,0),连接BC.点P是y轴上一动点,连接PA、PB,动点P从点C 出发,沿射线CO方向以每秒1个单位长度的速度运动,设运动时间为t(秒).
出发,沿射线CO方向以每秒1个单位长度的速度运动,设运动时间为t(秒).
(1)求抛物线对应的函数关系式.
(2)点P在运动的过程中,当S△ABP=S△CPB时,求t的值.
(3)点P在运动的过程中,△ABP与△CPB均为轴对称图形时,这样的t值有______个.
解:(1)将点C(0,4),点B(2,0)代入可得, ,
,
解得: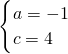 ,
,
故可得二次函数解析式为:y=-x2+4.
(2)①当点P在线段OC上时,
S△ABP= AB•OP=
AB•OP= 4×(4-t)=8-2t,S△CPB=
4×(4-t)=8-2t,S△CPB= CP×BO=t,
CP×BO=t,
∵S△ABP=S△CPB,
∴8-2t=t,
解得:t= ;
;
②当点P在x轴下方时,S△ABP= AB•OP=
AB•OP= 4×(t-4)=2t-8,S△CPB=
4×(t-4)=2t-8,S△CPB= CP×BO=t,
CP×BO=t,
∵S△ABP=S△CPB,
∴2t-8=t,
解得:t=8,
综上可得当t= 或8时,S△ABP=S△CPB.
或8时,S△ABP=S△CPB.
(3)当△CBP是等腰三角形时,可满足题意,
①BC=BP,②CP=CB,③PC=PB,

如图所示,满足题意得点P的坐标有三个.
分析:(1)将点C及点B的坐标代入即可得出a与c的值,继而可得出抛物线对应的函数关系式;
(2)分两种情况讨论,①点P在x轴上方,②点P在x轴下方,分别表示出△ABP及△CPB的面积,然后根据S△ABP=S△CPB,可得出关于t的方程,解出即可.
(3)△APB是轴对称图形,只需满足△CPB是轴对称图形即可,也就是只要△CPB是等腰三角形即可满足条件,分情况讨论,①BC=BP,②CP=CB,③PC=PB,分别作出图形即可得出答案.
点评:此题属于二次函数的综合题,涉及了待定系数法求二次函数解析式,等腰三角形的性质及轴对称的知识,解答本题的关键是掌握动点的移动速度与线段长度的关系.
 ,
,解得:
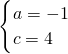 ,
,故可得二次函数解析式为:y=-x2+4.
(2)①当点P在线段OC上时,
S△ABP=
 AB•OP=
AB•OP= 4×(4-t)=8-2t,S△CPB=
4×(4-t)=8-2t,S△CPB= CP×BO=t,
CP×BO=t,∵S△ABP=S△CPB,
∴8-2t=t,
解得:t=
 ;
;②当点P在x轴下方时,S△ABP=
 AB•OP=
AB•OP= 4×(t-4)=2t-8,S△CPB=
4×(t-4)=2t-8,S△CPB= CP×BO=t,
CP×BO=t,∵S△ABP=S△CPB,
∴2t-8=t,
解得:t=8,
综上可得当t=
 或8时,S△ABP=S△CPB.
或8时,S△ABP=S△CPB.(3)当△CBP是等腰三角形时,可满足题意,
①BC=BP,②CP=CB,③PC=PB,

如图所示,满足题意得点P的坐标有三个.
分析:(1)将点C及点B的坐标代入即可得出a与c的值,继而可得出抛物线对应的函数关系式;
(2)分两种情况讨论,①点P在x轴上方,②点P在x轴下方,分别表示出△ABP及△CPB的面积,然后根据S△ABP=S△CPB,可得出关于t的方程,解出即可.
(3)△APB是轴对称图形,只需满足△CPB是轴对称图形即可,也就是只要△CPB是等腰三角形即可满足条件,分情况讨论,①BC=BP,②CP=CB,③PC=PB,分别作出图形即可得出答案.
点评:此题属于二次函数的综合题,涉及了待定系数法求二次函数解析式,等腰三角形的性质及轴对称的知识,解答本题的关键是掌握动点的移动速度与线段长度的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.