Question

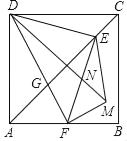
【题目】如图，正方形ABCD中，AD＝8，点E是对角线AC上一点，连接DE，过点E作EF⊥ED，交AB于点F，连接DF，交AC于点G，将△EFG沿EF翻折，得到△EFM，连接DM，交EF于点N，若点F是AB的中点，则（1）FM＝_____；（2）tan∠MDE＝_____．

Answer 1

【答案】

【解析】

（1）如图，过E作EP⊥AP，EQ⊥AD，根据正方形的性质得到∠EAQ=∠EAP=45°，推出四边形APEQ是正方形，根据全等三角形的性质得到DE=EF，DQ=FP，且AP=EP，设EP=x，则DQ=8-x=FP=x-4，根据勾股定理得到AE=，DE=，根据相似三角形的性质得到=2，过G作GH⊥AB，过M作MK⊥AB，过M作ML⊥AD，根据勾股定理得到结论；

（2）推出DM在正方形对角线DB上，过M作MK⊥AB，过N作NI⊥AB，则BK=MK=，根据平行线分线段成比例定理得到，求得FI=4-y=1，于是得到结论．

（1）如图，过E作EP⊥AP，EQ⊥AD，

∵四边形APEQ是正方形，

∴DC∥AB，

∴△DGC∽△FGA，

∴=2，

∵AC=8，DF=4

∴CG=，

∴EG==，

AG=AC=，

过G作GH⊥AB，过M作MK⊥AB，过M作ML⊥AD，

则易证△GHF≌△FKM全等，

∴GH=FK=，HF=MK=，

∴FM=；

∵ML=AK=AF+FK=4+=，DL=AD-MK=8-=，

即DL=LM，

∴∠LDM=45°

∴DM在正方形对角线DB上，

过N作NI⊥AB，则NI=IB，

设NI=y，

∵NI∥EP

∴，

∴，

解得y=3，

所以FI=4-y=1，

∴I为FP的中点，

∴N是EF的中点，

∴EN=EF=，

∵DF=4，

∴DE=2，

∴tan∠MDE=，

故答案为：，．