题目内容
 如图,在△ABC中,∠BAC=90°,∠ABC=45°,若MN是经过点A的直线,BD⊥MN于D,CE⊥MN于E,
如图,在△ABC中,∠BAC=90°,∠ABC=45°,若MN是经过点A的直线,BD⊥MN于D,CE⊥MN于E,(1)求证:BD=AE.
(2)若将MN绕点A旋转,使MN与BC相交于点O,其他条件都不变,(自己画出图)BD与AE边相等吗?为什么?
(3)请问:在(2)中条件下,BD、CE与DE有何关系?(直接写出)
考点:全等三角形的判定与性质
专题:
分析:(1)利用△ABD≌△CEA,可求出BD=AE,
(2)第二问中若将MN绕点A旋转,与BC相交于点O,则BD,CE与MN垂直,AB=AC,两个三角形仍全等,
(3)第三问利用△ABD≌△CEA,可确定三条线段之间的关系.
(2)第二问中若将MN绕点A旋转,与BC相交于点O,则BD,CE与MN垂直,AB=AC,两个三角形仍全等,
(3)第三问利用△ABD≌△CEA,可确定三条线段之间的关系.
解答:(1)证明:由题意可知,BD⊥MN与D,EC⊥MN与E,∠BAC=90°,
则△ABD与△CEA是直角三角形,∠DAB=∠ECA,
在△ABD与△CEA中,
∵
,
∴△ABD≌△CEA,
∴BD=AE;
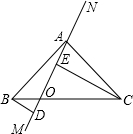
(2)若将MN绕点A旋转,与BC相交于点O,
则BD,CE与MN垂直,
∴△ABD与△CEA仍是直角三角形,两个三角形仍全等,
∴BD与AE边仍相等;
(3)∵△ABD≌△CEA,
∴BD=AE,AD=EC,
∴DE=BD+EC或DE=CE-BD或DE=BD-CE.
则△ABD与△CEA是直角三角形,∠DAB=∠ECA,
在△ABD与△CEA中,
∵
|
∴△ABD≌△CEA,
∴BD=AE;

(2)若将MN绕点A旋转,与BC相交于点O,
则BD,CE与MN垂直,
∴△ABD与△CEA仍是直角三角形,两个三角形仍全等,
∴BD与AE边仍相等;
(3)∵△ABD≌△CEA,
∴BD=AE,AD=EC,
∴DE=BD+EC或DE=CE-BD或DE=BD-CE.
点评:本题考查了直角三角形的边角关系,全等三角形的判定和性质等知识点,属中档题,做题时要从已知开始,结合相关知识认真思考.

练习册系列答案
相关题目
已知-2m6n与5m2xny是同类项,则( )
| A、X=2,y=1 | ||
| B、x=3,y=1 | ||
C、x=
| ||
| D、x=3 y=0 |
下列各组中的两个项不属于同类项的是( )
| A、3x2y和-2x2y | ||
| B、-xy和2yx | ||
C、-1和1
| ||
| D、a2b和ab2 |
甲型H1N1流感病毒是A型流感病毒,携带有H1N1亚型猪流感病毒毒株,包含有禽流感、猪流感和人流感三种流感病毒,预计今年全球将有约三千万人感染该病毒的危险.请用科学记数法表示:三千万( )
| A、3×106 |
| B、3×107 |
| C、3×108 |
| D、3×109 |
 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.