Question

如图1，已知菱形ABCD的边长为2，点A在x轴负半轴上，点B在坐标原点．点D的坐标为（﹣，3），抛物线y=ax²+b（a≠0）经过AB、CD两边的中点．

（1）求这条抛物线的函数解析式；

（2）将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移（如图2），过点B作BE⊥CD于点E，交抛物线于点F，连接DF、AF．设菱形ABCD平移的时间为t秒（0＜t＜）

①是否存在这样的t，使△ADF与△DEF相似？若存在，求出t的值；若不存在，请说明理由；

②连接FC，以点F为旋转中心，将△FEC按顺时针方向旋转180°，得△FE′C′，当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中（包括边界）时，求t的取值范围．（写出答案即可）

　

Answer 1

【考点】二次函数综合题．

【专题】压轴题．

【分析】（1）根据已知条件求出AB和CD的中点坐标，然后利用待定系数法求该二次函数的解析式；

（2）本问是难点所在，需要认真全面地分析解答：

①如图2所示，△ADF与△DEF相似，包括三种情况，需要分类讨论：

（I）若∠ADF=90°时，△ADF∽△DEF，求此时t的值；

（II）若∠DFA=90°时，△DEF∽△FBA，利用相似三角形的对应边成比例可以求得相应的t的值；

（III）∠DAF≠90°，此时t不存在；

②如图3所示，画出旋转后的图形，认真分析满足题意要求时，需要具备什么样的限制条件，然后根据限制条件列出不等式，求出t的取值范围．确定限制条件是解题的关键．

【解答】解：（1）由题意得AB的中点坐标为（﹣，0），CD的中点坐标为（0，3），

分别代入y=ax²+b得

，

解得，，

∴y=﹣x²+3．                                      

 

（2）①如图2所示，在Rt△BCE中，∠BEC=90°，BE=3，BC=2

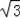
∴sinC===，∴∠C=60°，∠CBE=30°

∴EC=BC=，DE=

又∵AD∥BC，∴∠ADC+∠C=180°

∴∠ADC=180°﹣60°=120°

要使△ADF与△DEF相似，则△ADF中必有一个角为直角．

（I）若∠ADF=90°

∠EDF=120°﹣90°=30°

在Rt△DEF中，DE=，求得EF=1，DF=2．

又∵E（t，3），F（t，﹣t²+3），∴EF=3﹣（﹣t²+3）=t²

∴t²=1，∵t＞0，∴t=1                                     

此时=2，，

∴，

又∵∠ADF=∠DEF

∴△ADF∽△DEF                                 

（II）若∠DFA=90°，

可证得△DEF∽△FBA，则

设EF=m，则FB=3﹣m

∴，即m²﹣3m+6=0，此方程无实数根．

∴此时t不存在；                                       

（III）由题意得，∠DAF＜∠DAB=60°

∴∠DAF≠90°，此时t不存在．                             

综上所述，存在t=1，使△ADF与△DEF相似；

②如图3所示，依题意作出旋转后的三角形△FE′C′，过C′作MN⊥x轴，分别交抛物线、x轴于点M、点N．

观察图形可知，欲使△FE′C′落在指定区域内，必须满足：EE′≤BE且MN≥C′N．

∵F（t，3﹣t²），∴EF=3﹣（3﹣t²）=t²，∴EE′=2EF=2t²，

由EE′≤BE，得2t²≤3，解得t≤．

∵C′E′=CE=，∴C′点的横坐标为t﹣，

∴MN=3﹣（t﹣）²，又C′N=BE′=BE﹣EE′=3﹣2t²，

由MN≥C′N，得3﹣（t﹣）²≥3﹣2t²，解得t≥或t≤﹣﹣3（舍）．

∴t的取值范围为：．

【点评】本题是动线型中考压轴题，综合考查了二次函数的图象与性质、待定系数法、几何变换（平移与旋转）、菱形的性质、相似三角形的判定与性质等重要知识点，难度较大，对考生能力要求很高．本题难点在于第（2）问，（2）①中，需要结合△ADF与△DEF相似的三种情况，分别进行讨论，避免漏解；（2）②中，确定“限制条件”是解题关键．