题目内容
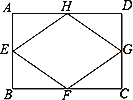
【题目】如图1,E为正方形ABCD的边BC上一点,F为边BA延长线上一点,且CE=AF.

(1)求证:DE⊥DF;
(2)如图2,若点G为边AB上一点,且∠BGE=2∠BFE,△BGE的周长为16,求四边形DEBF的面积;
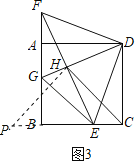
(3)如图3,在(2)的条件下,DG与EF交于点H,连接CH且CH=5![]() ,求AG的长.
,求AG的长.
【答案】(1)见解析;(2)64;(3)![]()
【解析】
(1)证明![]() ,根据全等三角形的性质得到
,根据全等三角形的性质得到![]() ,根据垂直的定义证明;
,根据垂直的定义证明;
(2)根据三角形的外角的性质、等腰三角形的判定定理得到![]() ,根据三角形的周长公式求出
,根据三角形的周长公式求出![]() ,根据正方形的面积公式计算;
,根据正方形的面积公式计算;
(3)作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,证明
,证明![]() ,得到
,得到![]() ,
,![]() ,根据勾股定理列方程求出
,根据勾股定理列方程求出![]() ,计算即可.
,计算即可.
(1)证明:![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() ;
;
(2)解:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 的周长为16
的周长为16
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
![]() ;
;
(3)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
![]() ,
,![]() ,
,
![]() 垂直平分
垂直平分![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
![]() 在四边形
在四边形![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
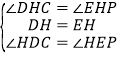 ,
,
![]()
![]() ,
,![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,设
中,设![]() ,则
,则![]() ,
,
由勾股定理得,![]()
解得:![]() ,
,
![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目