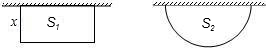题目内容
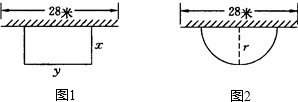
某农场计划建一个养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙(墙足够长),另外的部分用30米的竹篱笆围成,现有两种方案:①围成一个矩形(如下左图);②围成一个半圆形(如下右图),设矩形的面积为S1平方米,宽为x米,半圆形的面积为S2平方米,半径为r米,请你通过计算帮助农场主选择一个围成区域面积最大的方案(π≈3)。

解:S1=x(30-2x)
=-2x2+30x
=-2(x- )2+
)2+ ,
,
当x= 米时 S1取最大值
米时 S1取最大值 平方米,
平方米,
由30=πr得r=10米,
S2= πr2=
πr2= ×3×100=150平方米,
×3×100=150平方米,
∵ <150,
<150,
∴S1<S2,
∴应选择方案②。
=-2x2+30x
=-2(x-
 )2+
)2+ ,
,当x=
 米时 S1取最大值
米时 S1取最大值 平方米,
平方米,由30=πr得r=10米,
S2=
 πr2=
πr2= ×3×100=150平方米,
×3×100=150平方米,∵
 <150,
<150,∴S1<S2,
∴应选择方案②。

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目