题目内容
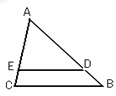
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
小题1:求证:∠DAF=∠CDE
小题2:问△ADF与△DEC相似吗?为什么?
小题3:若AB=4,AD=3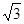 ,AE=3,求AF的长.
,AE=3,求AF的长.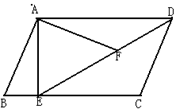
小题1:求证:∠DAF=∠CDE
小题2:问△ADF与△DEC相似吗?为什么?
小题3:若AB=4,AD=3
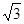 ,AE=3,求AF的长.
,AE=3,求AF的长.
小题1:见解析。
小题2:△ADF与△DEC相似
小题3:

(1)∵平行四边形ABCD∴AB∥CD∴∠B+∠C=180°;又∵∠B=∠AFE ∴∠C=∠AFD;
又∵∠DAF+∠AFD+∠ADF=180°; ∠CDE+∠C+∠ADF=180°;∴∠DAF=∠CDE
(2)△ADF与△DEC相似 ∵四边形ABCD是平行四边形 ∴AD∥BC AB∥CD ∴∠ADF=∠CED
∠B+∠C=180° ∵∠AFE+∠AFD=180°∠AFE=∠B ∴∠AFD=∠C ∴△ADF∽△DEC
(3)解:∵四边形ABCD是平行四边形
∴AD∥BC CD="AB=4" 又∵AE⊥BC ∴ AE⊥AD
在Rt△ADE中,DE=
∵△ADF∽△DEC ∴ ∴
∴ AF=
AF=
又∵∠DAF+∠AFD+∠ADF=180°; ∠CDE+∠C+∠ADF=180°;∴∠DAF=∠CDE
(2)△ADF与△DEC相似 ∵四边形ABCD是平行四边形 ∴AD∥BC AB∥CD ∴∠ADF=∠CED
∠B+∠C=180° ∵∠AFE+∠AFD=180°∠AFE=∠B ∴∠AFD=∠C ∴△ADF∽△DEC
(3)解:∵四边形ABCD是平行四边形
∴AD∥BC CD="AB=4" 又∵AE⊥BC ∴ AE⊥AD
在Rt△ADE中,DE=

∵△ADF∽△DEC ∴
 ∴
∴ AF=
AF=

练习册系列答案
相关题目
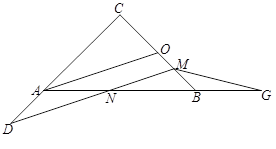
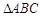 中,
中,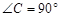 ,
,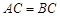 ,
,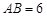 ,
,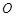 是
是 边上的中点,
边上的中点,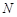 是
是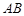 边上的点(不与端点重合),
边上的点(不与端点重合),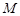 是
是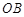 边上的点,且
边上的点,且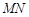 ∥
∥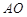 ,延长
,延长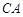 与直线
与直线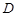 ,
,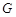 点是
点是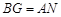 ,联结
,联结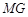 ,设
,设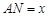 ,
,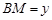 .
.
 关于
关于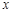 的函数关系式及其定义域;
的函数关系式及其定义域; ,当以
,当以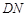 为半径的
为半径的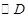 和以
和以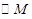 外切时,求
外切时,求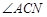 的正切值;
的正切值;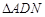 与
与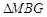 相似时,求
相似时,求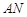 的长.
的长.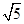 ;
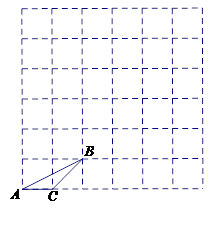
;
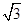 x和过x轴上的正奇数1、3、5、7、9、…所对应的点且与y轴平行的直线围成的.从左到右,将其面积依次记为S1、S2、S3、…、Sn、….则S1= ,Sn= .
x和过x轴上的正奇数1、3、5、7、9、…所对应的点且与y轴平行的直线围成的.从左到右,将其面积依次记为S1、S2、S3、…、Sn、….则S1= ,Sn= .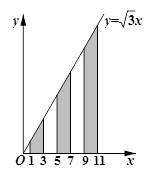



 = 。
= 。
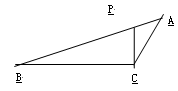
 DB,DE=3,求BC= 。
DB,DE=3,求BC= 。