题目内容
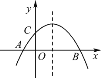
【题目】如图,已知抛物线![]() (m>0)与x轴相交于点A,B,与y轴相交于点C,且点A在点B的左侧.
(m>0)与x轴相交于点A,B,与y轴相交于点C,且点A在点B的左侧.
(1)若抛物线过点(2,2),求抛物线的解析式;
(2)在(1)的条件下,抛物线的对称轴上是否存在一点H,使AH+CH的值最小,若存在,求出点H的坐标;若不存在,请说明理由;
(3)在第四象限内,抛物线上是否存在点M,使得以点A,B,M为顶点的三角形与△ACB相似?若存在,求出m的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)点H的坐标为(1,
;(2)点H的坐标为(1,![]() );(3)当m=
);(3)当m=![]() 时,在第四象限内抛物线上存在点M,使得以点A,B,M为顶点的三角形与△ACB相似.
时,在第四象限内抛物线上存在点M,使得以点A,B,M为顶点的三角形与△ACB相似.
【解析】
(1)把点(2,2)代入![]() 中,解出m的值即可得到抛物线的解析式;
中,解出m的值即可得到抛物线的解析式;
(2)由(1)中所得解析式求出点A、B、C的坐标,由题意可知,点A、B关于抛物线的对称轴对称,这样连接BC与对称轴的交点即为所求的点H,根据B、C的坐标求出直线BC的解析式即可求得点H的坐标;
(3)由解析式![]() 可得点A、B、C的坐标分别为(-2,0)、(m,0)和(0,2),如下图,由图可知∠ACB和∠ABM是钝角,因此存在两种可能性:①当△ACB∽△ABM,②△ACB∽△MBA,分这两种情况结合题中已知条件进行分析解答即可.
可得点A、B、C的坐标分别为(-2,0)、(m,0)和(0,2),如下图,由图可知∠ACB和∠ABM是钝角,因此存在两种可能性:①当△ACB∽△ABM,②△ACB∽△MBA,分这两种情况结合题中已知条件进行分析解答即可.
(1)把点(2,2)代入抛物线,
得2=![]() .
.
解得m=4.
∴抛物线的解析式为![]() .
.
(2)令![]() ,解得
,解得![]() .
.
则A(-2,0),B(4,0).
对称轴x=-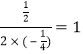 .
.
∵ ![]() 中当x=0时,y=2,
中当x=0时,y=2,
∴点C的坐标为(0,2).
∵点A和点B关于抛物线的对称轴对称,
∴连接BC与对称轴的交点即为点H,此时AH+CH的值最小,
设直线BC的解析式为y=kx+b,
把B(4,0),C(0,2)代入得:![]() ,解得:
,解得: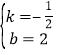 ,
,
∴直线BC的解析式为y=![]() .
.
∵当x=1时,y=![]() =
=![]() .
.
∴点H的坐标为(1,![]() ).
).
(3)假设存在点M,使得以点A,B,M为顶点的三角形与△ACB相似.
如下图,连接AC,BC,AM,BM,过点M作MN⊥x轴于点N,

由图易知,∠ACB和∠ABM为钝角,
①当△ACB∽△ABM时,有![]() =
=![]() ,即
,即![]() .
.
∵A(-2,0),C(0,2),即OA=OC=2,
∴∠CAB=∠BAM=![]() .
.
∵MN⊥x轴,∴∠BAM=∠AMN=45°,
∴AN=MN.
∴可设M的坐标为:(x,-x-2)(x>0),
把点M的坐标代入抛物线的解析式,得:-x-2=![]() .
.
化简整理得:x=2m,
∴点M的坐标为:(2m,-2m-2).
∴AM=![]() .
.
∵![]() ,AC=
,AC=![]() ,AB=m+2,
,AB=m+2,
∴![]() .
.
解得:m=![]() .
.
∵m>0,
∴m=![]() .
.
②当△ACB∽△MBA时,有![]() =
=![]() ,即
,即![]() .
.
∵∠CBA=∠BAM,∠ANM=∠BOC=![]() ,
,
∴△ANM∽△BOC,∴![]() =
=![]() .
.
∵BO=m,设ON=x,
∴![]() =
=![]() ,即MN=
,即MN=![]() (x+2).
(x+2).
令M(x,![]() )(x>0),
)(x>0),
把M点的坐标代入抛物线的解析式,
得![]() =
=![]() .
.
解得x=m+2.即M(m+2,![]() ).
).
∵![]() ,CB=
,CB=![]() ,MN=
,MN=![]() ,
,
∴![]() .
.
化简整理,得16=0,显然不成立.
综上所述,当m=![]() 时,在第四象限内抛物线上存在点M,使得以点A,B,M为顶点的三角形与△ACB相似.
时,在第四象限内抛物线上存在点M,使得以点A,B,M为顶点的三角形与△ACB相似.

【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.