题目内容
如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒
1.在点P、Q运动过程中,请判断PQ与对角线AC的位置关系,并说明理由;
2.若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①当t为何值时,点P、M、N在一直线上?
②当点P、M、N不在一直线上时,是否存在这样的t,使得△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.

1.若0<t≤5,则AP=4t,AQ=2t. 则 ==,
又 ∵ AO=10,AB=20,∴ ==.∴ =,
又 ∠CAB=30°,∴ △APQ∽△ABO,∴ ∠AQP=90°,即PQ⊥AC.………………4分
当5﹤t≤10时,同理可由△PCQ∽△BCO 可得∠PQC=90°,即PQ⊥AC(考虑一种情况即可) ∴ 在点P、Q运动过程中,始终有PQ⊥AC.
2.① 如图,在RtAPM中,易知AM=,又AQ=2t,
QM=20-4t.
由AQ+QM=AM 得2t+20-4t=
解得t=,∴ 当t=时,点P、M、N在一直线上. …………………………8分
② 存在这样的t,使△PMN是以PN为一直角边的直角三角形.
设l交AC于H.
如图1,当点N在AD上时,若PN⊥MN,则∠NMH=30°.
∴ MH=2NH,得 20-4t-=2× 解得t=2, …………………10分



如图2,当点N在CD上时,若PM⊥MN,则∠HMP=30°.∴ MH=2PH,同理可得t= .故 当t=2或 时,存在以PN为一直角边的直角三角形. …………………12分
解析:略

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案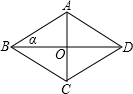 如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )
如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=α,则下列结论正确的是( )A、sinα=
| ||
B、cosα=
| ||
C、tanα=
| ||
D、tanα=
|
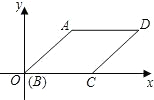 如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为
如图,菱形ABCD的边长为2,∠ABC=45°,则点D的坐标为 如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.
如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ交边AD于点E.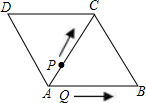 △ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).
△ABC重叠部分的面积为ycm2(规定:点和线段是面积为0的三角形).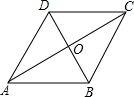 已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.
已知:如图,菱形ABCD的周长为8cm,∠ABC:∠BAD=2:1,对角线AC、BD相交于点O,求BD及AC的长.