题目内容
如图1,在平面直角坐标系中,点A的坐标为(1,2),点B的坐标为(3,1),二次函数y=x2的图象记为抛物线l1.
(1)平移抛物线l1,使平移后的抛物线过点A,但不过点B,写出平移后的一个抛物线的函数表达式(任写一个即可);
(2)平移抛物线l1,使平移后的抛物线过A,B两点,记为抛物线l2,如图2,求抛物线l2的函数表达式;
(3)设抛物线l2的顶点为C,K为y轴上一点.若S△ABK=S△ABC,求点K的坐标;
(4)请在图3上用尺规作图的方式探究抛物线l2上是否存在点P,使△ABP为等腰三角形.若存在,请判断点P共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.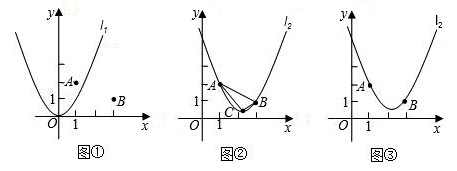
(1)有多种答案,符合条件即可.
例如y=x2+1,y=x2+x,y=(x-1)2+2或y=x2-2x+3,
y=(x+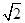 -1)2,y=(x-1-
-1)2,y=(x-1-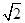 )2.
)2.
(2)设抛物线l2的函数表达式为y=x2+bx+c,
∵点A(1,2),B(3,1)在抛物线l2上,
∴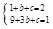 , 解得
, 解得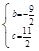 ,
,
∴抛物线l2的函数表达式为y=x2-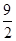 x+
x+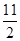 .
.
(3)y=x2-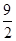 x+
x+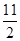 =(x-
=(x-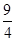 )2+
)2+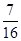 ,
,
∴C点的坐标为(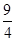 ,
,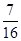 ).
).
过A,B,C三点分别作x轴的垂线,垂足分别为D,E,F,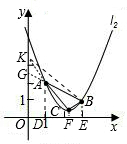
则AD=2,CF=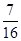 ,BE=1,DE=2,DF=
,BE=1,DE=2,DF=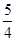 ,EF=
,EF=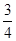 .
.
∴S△ABC=S梯形ADEB-S梯形ADFC-S梯形CFEB=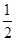 (2+1)×2-
(2+1)×2-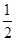 (2+
(2+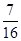 )×
)×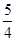 -
-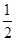 (1+
(1+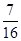 )×
)×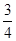 =
=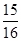 .
.
延长BA交y轴于点G,设直线AB的函数表达式为y=mx+n,
∵点A(1,2),B(3,1)在直线AB上,
∴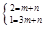 ,解得
,解得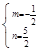 ,
,
∴直线AB的函数表达式为y=-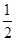 x+
x+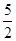 .
.
∴G点的坐标为(0,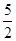 ).
).
设K点坐标为(0,h),分两种情况:
若K点位于G点的上方,则KG=h-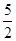 .
.
连接AK,BK.
S△ABK=S△BKG-S△AKG=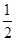 ×3×(h-
×3×(h-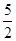 )-
)-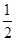 ×1×(h-
×1×(h-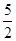 )=h-
)=h-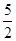 .
.
∵S△ABK=S△ABC=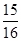 ,
,
∴h-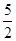 =
=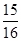 ,
,
解得h=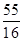 .
.
∴K点的坐标为(0,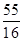 ).
).
若K点位于G点的下方,则KG=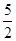 -h.
-h.
同理可得,h=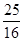 .
.
∴K点的坐标为(0,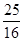 ).
).
(4)作图痕迹如图所示.
由图可知,点P共有4个可能的位置.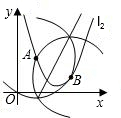
解析

 23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′;
23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′; 在平面直角坐标系中,将一块腰长为
在平面直角坐标系中,将一块腰长为

 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 再绕着点
再绕着点 点,这时点
点,这时点 与点
与点 为旋转中心时,点
为旋转中心时,点 点,点
点,点 点,点
点,点 点,小明发现P、
点,小明发现P、 两点关于点
两点关于点 中心对称.
中心对称.


 、
、 、
、 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到点
旋转180°得到点 . 继续如此操作若干次得到点
. 继续如此操作若干次得到点 ,则点
,则点 的坐为.
的坐为. ,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),
,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),