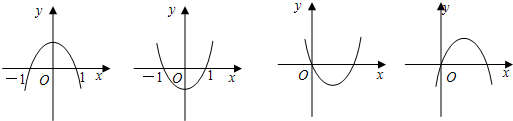题目内容
设a、b是常数，且b＞0，抛物线y=ax2+bx+a2-5a-6为图中两个图象之一，则a的值为（ ）分析：利用图象经过原点，则a2-5a-6=0，求出a的值，再利用两二次函数的对称轴经过x轴的正半轴，a，b异号，即可得出答案．
解答：解：由图象可得出：两图象经过原点，则a2-5a-6=0，
解得：a1=6，a2=-1，
∵两二次函数的对称轴经过x轴的正半轴，
∴a，b异号，
又∵b＞0，
∴a＜0，
∴a=-1．
故选：D．
解得：a1=6，a2=-1，
∵两二次函数的对称轴经过x轴的正半轴，
∴a，b异号，
又∵b＞0，
∴a＜0，
∴a=-1．
故选：D．
点评：此题主要考查了二次函数图象与系数的关系，利用已知得出a的符号是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
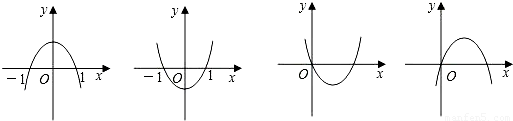
设a、b是常数，且b＞0，抛物线y=ax2+bx+a2-5a-6为下图中四个图象之一，则a的值为（ ）
| A、6或-1 | B、-6或1 | C、6 | D、-1 |
