��Ŀ����
����Ŀ��������̽����
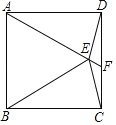
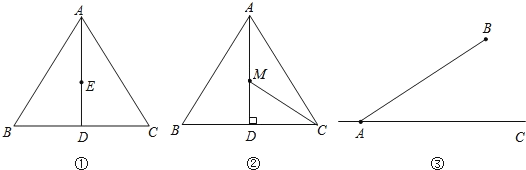
(1)��ͼ�٣���E������ABC��AD�ϵ�һ����,����AB����һ��F��ʹEF=![]() AE����˵�����ɣ�
AE����˵�����ɣ�
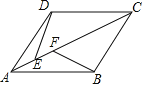
(2)��ͼ�ڣ���M�DZ߳�Ϊ2������ABC��AD�ϵ�һ���㣬��![]() AM+MC����Сֵ��
AM+MC����Сֵ��
����������
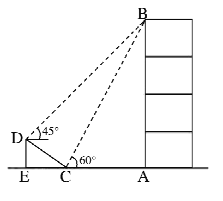
(3)��ͼ�ۣ�A��B�������600km,AC�DZ�ֱ���ض������������������һ����·����B��AC����̾���Ϊ360km����ƻ�����·��AC����һ����תվM������BM����һ����ֱ�Ĺ�·�����ͬ����������ÿǧ��·�ϵ��˷�����·�ϵ���������ô��Ϊʹͨ����·��A��M��ͨ����·��M��B�����˷Ѵﵽ��Сֵ����ȷ����תվM��λ��,�����AM�ij���(�����������)
���𰸡���1�������������2��![]() ����3��AM=(480
����3��AM=(480![]() )km��
)km��
��������
��1�����ݵȱ������ε����ʵó���BAD=30�����ó�EF=![]() AE��
AE��
��2����������ó�C��M��N��һ��ֱ����ʱ����ʱ![]() AM+MC��С������������ɣ�
AM+MC��С������������ɣ�
��3����BD��AC������Ϊ��D����AC���ڵ�B��һ������CAN=30������BF��AN������Ϊ��F����AC�ڵ�M����M��Ϊ������Rt��ABD�У����AD�ij�����Rt��MBD�У��ó�MD�ij������ɵó��𰸣�
�⣺(1)��ͼ������EF��AB������Ϊ��F����F��Ϊ����
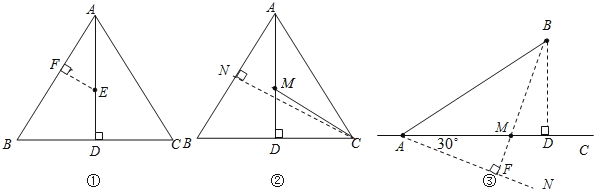
�������£��ߵ�E������ABC��AD�ϵ�һ���㣬
���BAD=30��
��EF��AB��
��EF=![]() AE��
AE��
(2)��ͼ��,��CN��AB,����Ϊ��N,��AD�ڵ�M,��ʱ![]() AM+MC��С����СΪCN�ij���
AM+MC��С����СΪCN�ij���
�ߡ�ABC�DZ߳�Ϊ2������ABC��
��CN=BCsin60=2��![]() =
=![]()
��MN+CM=12AM+MC=![]()
��![]() AM+MC����СֵΪ
AM+MC����СֵΪ![]()
(3)��ͼ��,��BD��AC,����Ϊ��D,��AC���ڵ�B��һ������CAN=30![]()
��BF��AN������Ϊ��F����AC�ڵ�M����M��Ϊ����
��Rt��ABD��,AD=![]() (km)
(km)
��Rt��MBD��,��MBD=��MAF=30,��MD=BDtan30=![]() (km)��
(km)��
����AM=(480![]() )km��
)km��

 �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�