题目内容
如图，点O在Rt△ABC的斜边AB上，⊙O切AC边于点E，切BC边于点D，连接OE，如果由线段CD、CE及劣弧ED围成的图形（阴影部分）面积与△AOE的面积相等，那么
的值约为（π取3.14）（ ）
| BC |
| AC |
| A．2.7 | B．2.5 | C．2.3 | D．2.1 |
如图，连接OD，
∵⊙O切AC边于点E，切BC边于点D，
∴∠ODC=∠OEC=∠C=90°，
∴四边形OECD是正方形，
而S阴影部分=S正方形OECD-S扇形ODE=OE2-
πOE2=S△AEO=
OE•AE，
∴OE：AE=
：（1-
），
∵OE∥BC，
∴
=
=
：（1-
）≈2.3．
故选C．
∵⊙O切AC边于点E，切BC边于点D，
∴∠ODC=∠OEC=∠C=90°，
∴四边形OECD是正方形，
而S阴影部分=S正方形OECD-S扇形ODE=OE2-
| 1 |
| 4 |
| 1 |
| 2 |
∴OE：AE=
| 1 |
| 2 |
| π |
| 4 |
∵OE∥BC，
∴
| BC |
| AC |
| OE |
| AE |
| 1 |
| 2 |
| π |
| 4 |
故选C．
练习册系列答案
相关题目
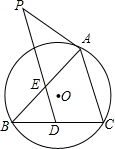
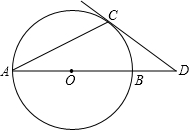
AC交BC于点D，在OD的延长线上取一点E，连接EB，使∠OEB=∠ABC．