题目内容
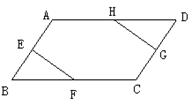
如图,在矩形ABCD中,点E、F在BC边上,且BE=CF,AF、DE交于点M.
求证:AM=DM.
求证:AM=DM.

∵四边形ABCD是矩形
∴AB="CD"
∠BAD=∠B=∠C=∠ADC=90 ………2分
………2分
∵BE=CF
∴BE+EF=CF+EF ………3分
∴△ABF △DCE ………4分
△DCE ………4分
∴∠BAF=∠CDE
∴∠DAF=∠ADE ………5分
∴AM=DM ………6分
∴AB="CD"
∠BAD=∠B=∠C=∠ADC=90
 ………2分
………2分∵BE=CF
∴BE+EF=CF+EF ………3分
∴△ABF
 △DCE ………4分
△DCE ………4分∴∠BAF=∠CDE
∴∠DAF=∠ADE ………5分
∴AM=DM ………6分
易证得△ABF≌△DCE,可得到∠AFB=∠DEC,利用矩形的对边平行的性质可求得它们的内错角也是相等的,进而得到AM=DM.

练习册系列答案
相关题目
 AFE是等腰三角形 ;(2)AF=BM.
AFE是等腰三角形 ;(2)AF=BM.



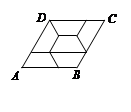


 BC,则四边形DBFE的面积为
BC,则四边形DBFE的面积为  .
.
