题目内容
如图,在Rt△ABC中,∠C=90°,AC=4,BC=5,D是BC边上一点,CD=3,点P在边AC上(点P与A、C不重合),过点P作PE∥BC,交AD于点E.
(1)设AP=x,DE=y,求y关于x的函数解析式,并写出x的取值范围;
(2)当以PE为半径的⊙E与DB为半径的⊙D外切时,求∠DPE的正切值;
(3)将△ABD沿直线AD翻折,得到△AB′D,连接B′C.如果∠ACE=∠BCB′,求AP的值.
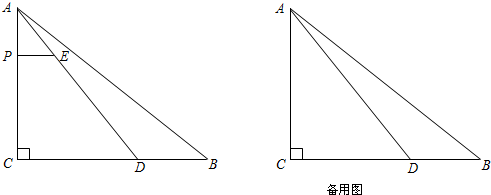
解:(1)∵在Rt△ABC中,AC=4,CD=3,
∴AD=5,
∵PE∥BC,
∴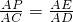 ,
,
∴ ,
,
∴AE= x,
x,
∴DE=5- x,
x,
即y=5- x,(0<x<4);
x,(0<x<4);
(2)当以PE为半径的⊙E与DB为半径的⊙D外切时,有DE=PE+BD,即5- x=
x= x+2,
x+2,
解之得x= ,
,
∴PC= ,
,
∵PE∥BC,
∴∠DPE=∠PDC,
在Rt△PCD中,
tan∠PDC=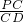 =
= =
= ;
;
∴tan∠DPE= ;
;
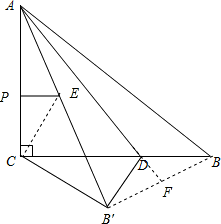 (3)延长AD交BB′于F,则AF⊥BB′,连接CE,
(3)延长AD交BB′于F,则AF⊥BB′,连接CE,
则∠ACD=∠BFD,
∵∠ADC=∠FDB,
∴∠CAD=∠FBD,
∴△ACD∽△BFD,
∴BF= ,
,
∴BB′= ,
,
∵∠ACE=∠BCB′,∠CAE=∠CBB′,
∴△ACE∽△BCB′,
∴AE= ,
,
∴t=AP=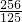 .
.
分析:(1)首先根据勾股定理求得AD的长,又由平行线分线段成比例定理求得DE的长,则可得y与x的关系;
(2)因为当以PE为半径的⊙E与DB为半径的⊙D外切时,有DE=PE+BD,所以可以求得x的值,即可求得PC的长,则在Rt△PCD中,根据三角函数的性质即可求得tan∠DPE的值;
(3)首先由有两角对应相等的三角形相似,即可证得:△ACD∽△BFD与△ACE∽△BCB′,又由相似三角形对应边成比例,即可求得AP的值.
点评:此题考查了相似三角形的判定与性质,以及旋转的性质,三角函数等知识.此题难度适中,解题的关键是注意数形结合思想的应用.
∴AD=5,
∵PE∥BC,
∴
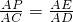 ,
,∴
 ,
,∴AE=
 x,
x,∴DE=5-
 x,
x,即y=5-
 x,(0<x<4);
x,(0<x<4);(2)当以PE为半径的⊙E与DB为半径的⊙D外切时,有DE=PE+BD,即5-
 x=
x= x+2,
x+2,解之得x=
 ,
,∴PC=
 ,
,∵PE∥BC,
∴∠DPE=∠PDC,
在Rt△PCD中,
tan∠PDC=
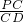 =
= =
= ;
;∴tan∠DPE=
 ;
; (3)延长AD交BB′于F,则AF⊥BB′,连接CE,
(3)延长AD交BB′于F,则AF⊥BB′,连接CE,则∠ACD=∠BFD,
∵∠ADC=∠FDB,
∴∠CAD=∠FBD,
∴△ACD∽△BFD,
∴BF=
 ,
,∴BB′=
 ,
,∵∠ACE=∠BCB′,∠CAE=∠CBB′,
∴△ACE∽△BCB′,
∴AE=
 ,
,∴t=AP=
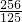 .
.分析:(1)首先根据勾股定理求得AD的长,又由平行线分线段成比例定理求得DE的长,则可得y与x的关系;
(2)因为当以PE为半径的⊙E与DB为半径的⊙D外切时,有DE=PE+BD,所以可以求得x的值,即可求得PC的长,则在Rt△PCD中,根据三角函数的性质即可求得tan∠DPE的值;
(3)首先由有两角对应相等的三角形相似,即可证得:△ACD∽△BFD与△ACE∽△BCB′,又由相似三角形对应边成比例,即可求得AP的值.
点评:此题考查了相似三角形的判定与性质,以及旋转的性质,三角函数等知识.此题难度适中,解题的关键是注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F. 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离. 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直. 如图,在Rt△ABC中,BD⊥AC,sinA=
如图,在Rt△ABC中,BD⊥AC,sinA= 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).