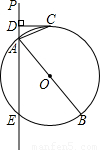
题目内容
已知:如图,直线PA交⊙O于A、E两点,PA的垂线DC切⊙O于点C,过A点作⊙O的直径AB.(1)求证:AC平分∠DAB;
(2)若DC=4,DA=2,求⊙O的直径.
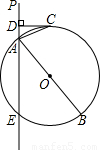
【答案】分析:(1)由弦切角定理知,∠DCA=∠B,故Rt△ADC∽Rt△ACB,则有∠DAC=∠CAB;
(2)由勾股定理求得AC的值后,由(1)中Rt△ADC∽Rt△ACB得 =
= ,即可求得AB的值.
,即可求得AB的值.
解答: (1)证明:方法一:连接BC,
(1)证明:方法一:连接BC,
∵AB为⊙O的直径,
∴∠ACB=90°,
又∵DC切⊙O于C点,
∴∠DCA=∠B,
∵DC⊥PE,
∴Rt△ADC∽Rt△ACB,
∴∠DAC=∠CAB,即AC平分∠DAB;
 方法二:连接CO,
方法二:连接CO,
因为DC与⊙O相切,
所以DC⊥CO,
又因为PA⊥CD,
所以CO∥PE,
所以∠ACO=∠CAO=∠CAD,即AC平分∠DAB
(2)解:在Rt△ADC中,AD=2,DC=4,
∴AC= =2
=2 ,
,
由(1)得Rt△ADC∽Rt△ACB,
∴ =
= ,
,
即AB= =
= =10,
=10,
∴⊙O的直径为10.
点评:本题的解法不唯一,可利用弦切角定理,直径对的圆周角是直角,切线的性质,相似三角形的判定和性质,勾股定理求解.
(2)由勾股定理求得AC的值后,由(1)中Rt△ADC∽Rt△ACB得
 =
= ,即可求得AB的值.
,即可求得AB的值.解答:
 (1)证明:方法一:连接BC,
(1)证明:方法一:连接BC,∵AB为⊙O的直径,
∴∠ACB=90°,
又∵DC切⊙O于C点,
∴∠DCA=∠B,
∵DC⊥PE,
∴Rt△ADC∽Rt△ACB,
∴∠DAC=∠CAB,即AC平分∠DAB;
 方法二:连接CO,
方法二:连接CO,因为DC与⊙O相切,
所以DC⊥CO,
又因为PA⊥CD,
所以CO∥PE,
所以∠ACO=∠CAO=∠CAD,即AC平分∠DAB
(2)解:在Rt△ADC中,AD=2,DC=4,
∴AC=
 =2
=2 ,
,由(1)得Rt△ADC∽Rt△ACB,
∴
 =
= ,
,即AB=
 =
= =10,
=10,∴⊙O的直径为10.
点评:本题的解法不唯一,可利用弦切角定理,直径对的圆周角是直角,切线的性质,相似三角形的判定和性质,勾股定理求解.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
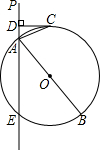 已知:如图,直线PA交⊙O于A、E两点,PA的垂线DC切⊙O于点C,过A点作⊙O的直径AB.
已知:如图,直线PA交⊙O于A、E两点,PA的垂线DC切⊙O于点C,过A点作⊙O的直径AB. (2013•丰台区二模)已知:如图,直线PA交⊙O于A、B两点,AE是⊙O的直径,点C是⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂足为点D.
(2013•丰台区二模)已知:如图,直线PA交⊙O于A、B两点,AE是⊙O的直径,点C是⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂足为点D.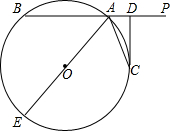 已知:如图,直线PA交⊙O于A、B两点,AE是⊙O的直径,点C是⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂足为点D.
已知:如图,直线PA交⊙O于A、B两点,AE是⊙O的直径,点C是⊙O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂足为点D. ,⊙O的直径为10,求AB的长.
,⊙O的直径为10,求AB的长.