题目内容
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线 (x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(1)如果b=-2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式。

 (x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。
(x>0)交于D点,过点D作DC⊥x轴,垂足为C,连接OD。已知△AOB≌△ACD。(1)如果b=-2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式。

(1)4; (2)y=x.
试题分析:(1)首先求出直线y=2x-2与坐标轴交点的坐标,然后由△AOB≌△ACD得到CD=OB,AO=AC,即可求出D坐标,由点D在双曲线y=
 ( x>0)的图象上求出k的值;
( x>0)的图象上求出k的值;(2)首先直线y=2x+b与坐标轴交点的坐标为A(-
 ,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式.
,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式.(1)当b=-2时,
直线y=2x-2与坐标轴交点的坐标为A(1,0),B(0,-2).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(2,2).
∵点D在双曲线y=
 ( x>0)的图象上,
( x>0)的图象上,∴k=2×2=4.
(2)直线y=2x+b与坐标轴交点的坐标为A(-
 ,0),B(0,b).
,0),B(0,b).∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(-b,-b).
∵点D在双曲线y=
 ( x>0)的图象上,
( x>0)的图象上,∴k=(-b)•(-b)=b2.
即k与b的数量关系为:k=b2.
直线OD的解析式为:y=x.

练习册系列答案
相关题目
 和
和 时,y关于t的函数关系式:
时,y关于t的函数关系式:
 是一张放在平面直角坐标系中的矩形纸片,
是一张放在平面直角坐标系中的矩形纸片, 为原点,点
为原点,点 在
在 轴的正半轴上,
轴的正半轴上, ,在
,在 上取一点
上取一点 ,将纸片沿
,将纸片沿 翻折,使点
翻折,使点 边上的点
边上的点 处,求直线
处,求直线 的解析式.
的解析式.
 (千米)与时间
(千米)与时间 (小时)之间函数关系的大致图象是( )。
(小时)之间函数关系的大致图象是( )。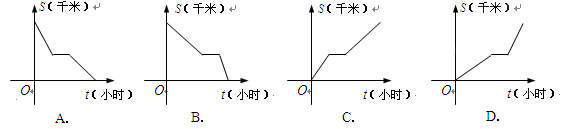
 与坐标轴交于A,C两点,过A,O,C三点作⊙O1,点E为劣弧AO上一点,连接EC,EA,EO,当点E在劣弧AO上运动时(不与A,O两点重合),
与坐标轴交于A,C两点,过A,O,C三点作⊙O1,点E为劣弧AO上一点,连接EC,EA,EO,当点E在劣弧AO上运动时(不与A,O两点重合), 的值是否发生变化?( )
的值是否发生变化?( )

 的图象与x轴交于点A,与y轴交于点B,与反比例函数
的图象与x轴交于点A,与y轴交于点B,与反比例函数 的图象在第一象限内交于点C,CD⊥x轴于点D,OD=2AO,求反比例函数
的图象在第一象限内交于点C,CD⊥x轴于点D,OD=2AO,求反比例函数 的表达式.
的表达式. 
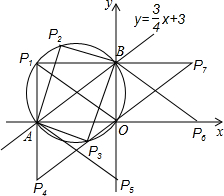
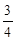 x+3与两坐标轴交于A、B两点,点O为坐标原点,若在该坐标平面内有以点P(不与点A、B、O重合)为顶点的直角三角形与Rt△ABO全等,且这个以点P为顶点的直角三角形与Rt△ABO有一条公共边,则所有符合条件的P点个数为( )
x+3与两坐标轴交于A、B两点,点O为坐标原点,若在该坐标平面内有以点P(不与点A、B、O重合)为顶点的直角三角形与Rt△ABO全等,且这个以点P为顶点的直角三角形与Rt△ABO有一条公共边,则所有符合条件的P点个数为( )