题目内容
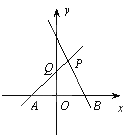
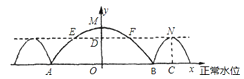
【题目】如图，三孔桥横截面的三个孔都呈抛物线形，两小孔形状、大小都相同．正常水位时，大孔水面宽度
米，顶点
距水面
米（即
米），小孔顶点
距水面
米（即
米）．当水位上涨刚好淹没小孔时，借助图中的直角坐标系，则此时大孔的水面宽度
长为（ ）
A. 
米 B. 
C. 
米 D. 
米
【答案】D
【解析】
根据题意，可以得到A、B、M的坐标，设出函数关系式，待定系数求解函数式．根据NC的长度，得出函数的y坐标，代入解析式，即可得出E、F的坐标，进而得出答案．
由题意得,M点坐标为(0,6),A点坐标为(10,0),B点坐标为(10,0)，
设中间大抛物线的函数式为
代入三点的坐标得到
解得
∴函数式为
∵NC=4.5米，
∴令y=4.5米，
代入解析式得
∴可得EF=5(5)=10米.
故选:D.
练习册系列答案
相关题目
