题目内容
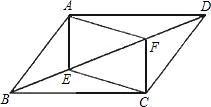
 如图,E,F是平行四边形ABCD对角线BD上的两点,在下列条件:①∠BAE=∠DCF,②BE=DF,③AE=CF,④AF=CE,⑤∠DAF=∠BCE,⑥AF∥CE,⑦AE⊥BD,CF⊥BD中,请你添加一个适当的条件,使四边形AECF是平行四边形,则还需要可添加的条件有个.
如图,E,F是平行四边形ABCD对角线BD上的两点,在下列条件:①∠BAE=∠DCF,②BE=DF,③AE=CF,④AF=CE,⑤∠DAF=∠BCE,⑥AF∥CE,⑦AE⊥BD,CF⊥BD中,请你添加一个适当的条件,使四边形AECF是平行四边形,则还需要可添加的条件有个.
- A.4
- B.5
- C.6
- D.7
A
分析:此题利用平行四边形的判定及全等三角形的性质求解.
解答: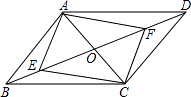 解:根据平行四边形的判定,对边平行且相等的四边形为平行四边形,
解:根据平行四边形的判定,对边平行且相等的四边形为平行四边形,
①∠BAE=∠DCF,若添加AE⊥BD,CF⊥BD,可以证明四边形AECF是平行四边形;
②BE=DF,根据四边形ABCD是平行四边形可证四边形AECF是平行四边形,不用添加;
③AE=CF,由△ABE≌△CDF的对应角相等推知∠AEB=∠CFD,则内错角∠AEF=∠CFE,所以AE∥CF,所以根据对边平行且相等的四边形是平行四边形可以证得四边形AECF是平行四边形,不用添加;
④AF=CE,添加AF∥CE可证四边形AECF是平行四边形;
⑤∠DAF=∠BCE,若添加AE⊥BD,CF⊥BD,可以证明四边形AECF是平行四边形;
⑥AF∥CE,添加AF=CE可得四边形AECF是平行四边形;
⑦AE⊥BD,CF⊥BD,根据四边形ABCD是平行四边形可证四边形AECF是平行四边形,不用添加;
∴可添加的条件有4个.
故选A.
点评:此题主要考查平行四边形的定义及其判定,熟练掌握平行四边形的性质及判定,则比较简单.
分析:此题利用平行四边形的判定及全等三角形的性质求解.
解答:
 解:根据平行四边形的判定,对边平行且相等的四边形为平行四边形,
解:根据平行四边形的判定,对边平行且相等的四边形为平行四边形,①∠BAE=∠DCF,若添加AE⊥BD,CF⊥BD,可以证明四边形AECF是平行四边形;
②BE=DF,根据四边形ABCD是平行四边形可证四边形AECF是平行四边形,不用添加;
③AE=CF,由△ABE≌△CDF的对应角相等推知∠AEB=∠CFD,则内错角∠AEF=∠CFE,所以AE∥CF,所以根据对边平行且相等的四边形是平行四边形可以证得四边形AECF是平行四边形,不用添加;
④AF=CE,添加AF∥CE可证四边形AECF是平行四边形;
⑤∠DAF=∠BCE,若添加AE⊥BD,CF⊥BD,可以证明四边形AECF是平行四边形;
⑥AF∥CE,添加AF=CE可得四边形AECF是平行四边形;
⑦AE⊥BD,CF⊥BD,根据四边形ABCD是平行四边形可证四边形AECF是平行四边形,不用添加;
∴可添加的条件有4个.
故选A.
点评:此题主要考查平行四边形的定义及其判定,熟练掌握平行四边形的性质及判定,则比较简单.

练习册系列答案
相关题目
 8、
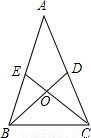
8、 1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
 相交于点C.
相交于点C.
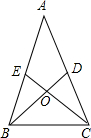 1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
1、如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.