Question

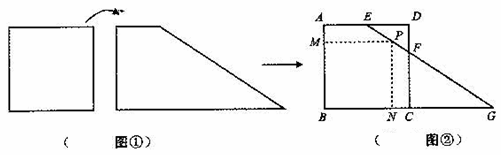
如图1是一块长为60cm的正方体薄铁片制作的一个长方体盒子，如果要做一个没有盖的长方体盒子，可先在薄铁片的四个角上截去四个相同的小正方形（如图2），然后把四边折合起来．
（1）求做成的盒子底面积y（cm²）与截去小正方形边长x（cm²）之间的函数关系式；
（2）当做成的盒子的底面积为900cm²时，试求该盒子的容积．

Answer 1

分析：（1）由底面积=大正方形的面积-四个小正方形的面积就可以得出结论；
（2）将y=900代入（1）的解析式就可以求出x的值，再由容积公式就可以得出结论．

解答：解：（1）由题意，得
y=60×60-4x²，
y=3600-4x²
∴做成的盒子底面积y（cm²）与截去小正方形边长x（cm²）之间的函数关系式为y=3600-4x²；

（2）当y=900时，
900=3600-4x²，
x=±15

3

．
∵x＞0，
∴x=15

3

．
∴盒子的容积为：15

3

×900=13500

3

；
答：盒子的容积为13500

3

．

点评：本题考查了正方形的面积公式的运用，一元二次方程的解法的运用，长方体容器的容积的运用，解答时求出容器的高是解答的关键．