题目内容
一个口袋内装有红、蓝、白三种不同颜色的小球,其中蓝球数至少是白球数的一半,但至多是红球数的 ,白球与蓝球的总和至少是55个,则红球至少有________个.
,白球与蓝球的总和至少是55个,则红球至少有________个.
57
分析:设红、蓝、白三种小球的个数分别为x,y,z,根据蓝球数至少是白球数的一半,但至多是红球数的 ,白球与蓝球的总和至少是55个,得到3个关系式,由第一个关系式可得用字母y表示z的式子,代入第3个不等式可得y的取值,进而可得红球的最小整数解.
,白球与蓝球的总和至少是55个,得到3个关系式,由第一个关系式可得用字母y表示z的式子,代入第3个不等式可得y的取值,进而可得红球的最小整数解.
解答:设红、蓝、白三种小球的个数分别为x,y,z.则
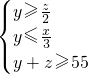 ,
,
由第一个不等式得z≤2y,
∴y+z≤y+2y=3y
∵y+z≥55,
∴3y≥55,
y≥18 ,
,
∴y的最小值是19,
∴x≥3y=57,
∴红球至少有57个.
故答案为57.
点评:本题考查了一元一次不等式组的应用,根据球的总数的关系式利用消元的方法求解是解决本题的关键.
分析:设红、蓝、白三种小球的个数分别为x,y,z,根据蓝球数至少是白球数的一半,但至多是红球数的
 ,白球与蓝球的总和至少是55个,得到3个关系式,由第一个关系式可得用字母y表示z的式子,代入第3个不等式可得y的取值,进而可得红球的最小整数解.
,白球与蓝球的总和至少是55个,得到3个关系式,由第一个关系式可得用字母y表示z的式子,代入第3个不等式可得y的取值,进而可得红球的最小整数解.解答:设红、蓝、白三种小球的个数分别为x,y,z.则
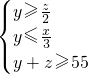 ,
,由第一个不等式得z≤2y,
∴y+z≤y+2y=3y
∵y+z≥55,
∴3y≥55,
y≥18
 ,
,∴y的最小值是19,
∴x≥3y=57,
∴红球至少有57个.
故答案为57.
点评:本题考查了一元一次不等式组的应用,根据球的总数的关系式利用消元的方法求解是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目