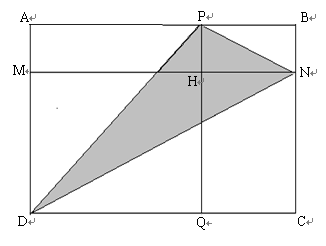
题目内容
 如图,若长方形APHM、BNHP、CQHN的面积分别是7、4、6,则△PDN的面积是
如图,若长方形APHM、BNHP、CQHN的面积分别是7、4、6,则△PDN的面积是8.5
8.5
.分析:利用长方形APHM、BNHP、CQHN的面积分别是7、4、6,得出长方形BNHP、CQHN的面积比,进而得出长方形MDQH,进而得出S△ADP,S△DCN,S△PBN的面积之和,即可得出△PDN的面积.
解答:解:根据长方形APHM、BNHP、CQHN的面积分别是7、4、6,
则长方形BNHP、CQHN的面积比为:4:6,
长方形APHM的面积是7,
∴长方形MDQH的面积为:
=
,
解得:长方形MDQH的面积=10.5.
故四边形ADQP的面积为:10.5+7=17.5,
S△ADP=
四边形ADQP的面积=
,
四边形MDCN的面积为:10.5+6=16.5,
S△DCN=
四边形MDCN的面积=
,
得出四边形ABCD的面积-(S△ADP+S△DCN+S△PBN)=S△PDN=(10.5+7+6+4)-(
+
+2)=8.5.
故答案为:8.5.
则长方形BNHP、CQHN的面积比为:4:6,
长方形APHM的面积是7,
∴长方形MDQH的面积为:
| 4 |
| 6 |
| 7 |
| 长方形MDQH的面积 |
解得:长方形MDQH的面积=10.5.
故四边形ADQP的面积为:10.5+7=17.5,
S△ADP=
| 1 |
| 2 |
| 35 |
| 4 |
四边形MDCN的面积为:10.5+6=16.5,
S△DCN=
| 1 |
| 2 |
| 33 |
| 4 |
得出四边形ABCD的面积-(S△ADP+S△DCN+S△PBN)=S△PDN=(10.5+7+6+4)-(
| 35 |
| 4 |
| 33 |
| 4 |
故答案为:8.5.
点评:此题主要考查了矩形性质以及三角形面积求法,利用矩形性质得出四边形ABCD的面积-(S△ADP+S△DCN+S△PBN)=S△PDN是解题关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 如图,若长方形APHM,BNHP,CQHN的面积分别为7、4、6,求阴影部分的面积是多少?
如图,若长方形APHM,BNHP,CQHN的面积分别为7、4、6,求阴影部分的面积是多少?