题目内容
如图，D、E分别是⊙O半径OA、OB上的点，CD⊥OA、CE⊥OB、CD=CE，则弧AC的长与弧CB的长的大小关系是
- A.
=
- B.＞
- C.＜
- D.不能确定
A
分析：根据直角三角形的判定定理HL，可得出△COD≌△C0E，则∠COD=∠COE，再根据在同圆中，相等的圆心角所对的弧也相等得出结论．
解答：∵CD⊥OA、CE⊥OB，
∴∠CDO=∠CEO=90°，
∵CD=CE，CO=CO，
∴△COD≌△C0E，
∴∠COD=∠COE，
∴=，
故选A．
点评：本题考查了圆心角、弧、弦之间的关系，以及全等三角形的判定和性质，是基础知识要熟练掌握．
分析：根据直角三角形的判定定理HL，可得出△COD≌△C0E，则∠COD=∠COE，再根据在同圆中，相等的圆心角所对的弧也相等得出结论．
解答：∵CD⊥OA、CE⊥OB，
∴∠CDO=∠CEO=90°，
∵CD=CE，CO=CO，
∴△COD≌△C0E，
∴∠COD=∠COE，
∴
=，故选A．
点评：本题考查了圆心角、弧、弦之间的关系，以及全等三角形的判定和性质，是基础知识要熟练掌握．
练习册系列答案
阅读快车系列答案
相关题目
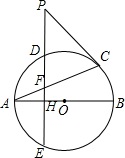如图：AB、AC分别是⊙O的直径和弦，D为弧AC上一点，DE⊥AB于点H，交⊙O于点E，交AC于点F．P为ED延长线上一点，连PC．
如图，AB和AC分别是⊙O的直径和弦，OD⊥AC于D点，若OA=4，∠A=30°，则BD等于（ ）
已知：如图，E、F分别是正方形ABCD边BC、AD上的点，且BE=DF
桌上放着一个圆柱和一个长方体，如图（1），请说出下列三幅图（如图（2））分别是从哪个方向看到的．