题目内容
（1）已知实数a，b满足a（a+1）-（a2+2b）=1，求a2-4ab+4b2-2a+4b的值．（2）如图是一个中心对称图形，A为对称中心，若∠C=90°，∠B=30°，BC=1，则BB′的长？
分析：（1）首先将已知条件化简，进而得出a-2b=1，再将原式变形得出即可；
（2）首先利用勾股定理得出AC的长，进而得出AC和AB的长，即可得出BB′的长．
（2）首先利用勾股定理得出AC的长，进而得出AC和AB的长，即可得出BB′的长．
解答：解：（1）∵a（a+1）-（a2+2b）=1，
∴等式变形得：a-2b=1；
原式=（a-2b）2-2（a-2b）=12-2=-1；
（2）设AC=x，AB=2x，BB′=4x，
在Rt△ABC中
AB2=AC2+BC2，
∴（2x）2=x2+12，
解得：x=±
（负数舍去），
∴AB=2×
=
，
∴BB′=
．
∴等式变形得：a-2b=1；
原式=（a-2b）2-2（a-2b）=12-2=-1；
（2）设AC=x，AB=2x，BB′=4x，
在Rt△ABC中
AB2=AC2+BC2，
∴（2x）2=x2+12，
解得：x=±
| ||
| 3 |
∴AB=2×
| ||
| 3 |
2
| ||
| 3 |
∴BB′=
4
| ||
| 3 |
点评：此题主要考查了中心对称以及勾股定理和整式的混合运算，正确将已知条件变形得出是解题关键．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
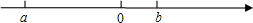已知实数a、b在数轴上的位置如图．