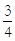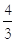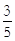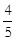题目内容
如图,直角梯形ABCD中,AD∥BC,∠A=90°,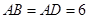 ,
,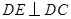 交AB于E,DF平分∠EDC交BC于F,连结EF.
交AB于E,DF平分∠EDC交BC于F,连结EF.
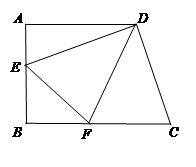
(1)证明: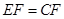 ;
;
(2)当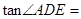
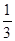 时,求EF的长.
时,求EF的长.
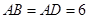 ,
,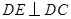 交AB于E,DF平分∠EDC交BC于F,连结EF.
交AB于E,DF平分∠EDC交BC于F,连结EF.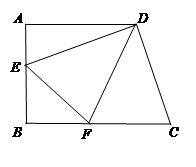
(1)证明:
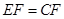 ;
;(2)当
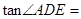
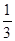 时,求EF的长.
时,求EF的长.(1)见解析(2)5
解:(1)过D作DG⊥BC于G.
由已知可得,四边形ABGD为正方形. …………1分
∵DE⊥DC,
∴∠ADE+∠EDG=90°=∠GDC+∠EDG,
∴∠ADE="∠GDC" . ………………………3分
又∵∠A=∠DGC,且AD=GD,
∴△ADE≌△GDC .
∴DE=DC,且AE=GC. ……………………4分
在△EDF和△CDF中,
∠EDF=∠CDF,DE=DC,DF为公共边,
∴△EDF≌△CDF.
∴EF="CF" . ……………………………………………6分
(2)∵tan∠ADE= =
=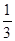 , ∴
, ∴ . ………………………………………9分
. ………………………………………9分
设 ,则
,则 ,BE=6-2="4."
,BE=6-2="4."
由勾股定理,得 .
.
解之,得 , 即
, 即 . ……………………………12分
. ……………………………12分
(1)作DG⊥BC,由已知可得,四边形ABGD为正方形,先证得△ADE≌△GDC,得到DE=DC,再有∠EDF=∠CDF,DF为公共边,可得△EDF≌△CDF,从而EF=CF.
(2)由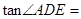
 =
=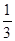 ,可得
,可得 ,再由勾股定理即可求出EF的长。
,再由勾股定理即可求出EF的长。
由已知可得,四边形ABGD为正方形. …………1分
∵DE⊥DC,
∴∠ADE+∠EDG=90°=∠GDC+∠EDG,
∴∠ADE="∠GDC" . ………………………3分
又∵∠A=∠DGC,且AD=GD,
∴△ADE≌△GDC .
∴DE=DC,且AE=GC. ……………………4分
在△EDF和△CDF中,
∠EDF=∠CDF,DE=DC,DF为公共边,
∴△EDF≌△CDF.
∴EF="CF" . ……………………………………………6分
(2)∵tan∠ADE=
 =
=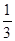 , ∴
, ∴ . ………………………………………9分
. ………………………………………9分设
 ,则
,则 ,BE=6-2="4."
,BE=6-2="4." 由勾股定理,得
 .
. 解之,得
 , 即
, 即 . ……………………………12分
. ……………………………12分(1)作DG⊥BC,由已知可得,四边形ABGD为正方形,先证得△ADE≌△GDC,得到DE=DC,再有∠EDF=∠CDF,DF为公共边,可得△EDF≌△CDF,从而EF=CF.
(2)由
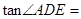
 =
=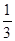 ,可得
,可得 ,再由勾股定理即可求出EF的长。
,再由勾股定理即可求出EF的长。
练习册系列答案
相关题目
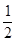 ,则∠A= ;若a=5,c=13,则tanA=
,则∠A= ;若a=5,c=13,则tanA= 

 .
.


 ,sin60
,sin60