题目内容
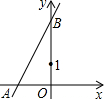 如图,直线y=2x+3与x轴交于点A,与y轴交于点B.
如图,直线y=2x+3与x轴交于点A,与y轴交于点B.(1)求A、B两点的坐标;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.
分析:(1)由函数解析式y=2x+3,令y=0求得A点坐标,x=0求得B点坐标;
(2)有两种情况,若BP与x轴正方向相交于P点,则AP=3OA;若BP与x轴负方向相交于P点,则AP=OA,由此求得△ABP的面积.
(2)有两种情况,若BP与x轴正方向相交于P点,则AP=3OA;若BP与x轴负方向相交于P点,则AP=OA,由此求得△ABP的面积.
解答:解:(1)令y=0,得x=-
,
∴A点坐标为(-
,0),
令x=0,得y=3,
∴B点坐标为(0,3);
(2)设P点坐标为(x,0),
∵OP=2OA,A(-
,0),
∴x=±3,
∴P点坐标分别为P1(3,0)或P2(-3,0).
∴S△ABP1=
×(
+3)×3=
,S△ABP2=
×(3-
)×3=
,
∴△ABP的面积为
或
| 3 |
| 2 |
∴A点坐标为(-
| 3 |
| 2 |
令x=0,得y=3,
∴B点坐标为(0,3);
(2)设P点坐标为(x,0),
∵OP=2OA,A(-
| 3 |
| 2 |
∴x=±3,
∴P点坐标分别为P1(3,0)或P2(-3,0).
∴S△ABP1=
| 1 |
| 2 |
| 3 |
| 2 |
| 27 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
∴△ABP的面积为
| 27 |
| 4 |
| 9 |
| 4 |
点评:此题主要考查了函数图象中坐标的求法以及面积的求法.

练习册系列答案
相关题目
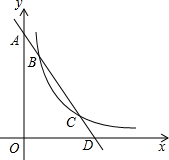 如图,直线y=-2x+b与y轴交于点A,与x轴交于点D,与双曲线
如图,直线y=-2x+b与y轴交于点A,与x轴交于点D,与双曲线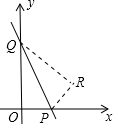 如图,直线y=-2x+6与x轴、y轴分别交于P、Q两点,把△POQ沿PQ翻折,点O落在R处,则点R的坐标是
如图,直线y=-2x+6与x轴、y轴分别交于P、Q两点,把△POQ沿PQ翻折,点O落在R处,则点R的坐标是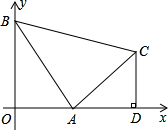 腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D.
腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D. 轴分别交于点C、D.直线EB交x轴于点F.
轴分别交于点C、D.直线EB交x轴于点F. 如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.
如图,直线y=-2x+8与两坐标轴分别交于P,Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.