��Ŀ����
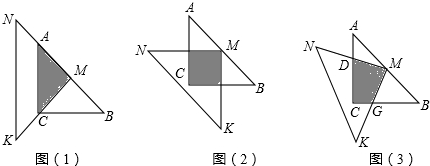
һλͬѧ��������45�����dzߡ�MNK����ACB����һ��̽���������MNK��ֱ�Ƕ���M���ڡ�ABC��б��AB���е㴦����AC=BC=4��
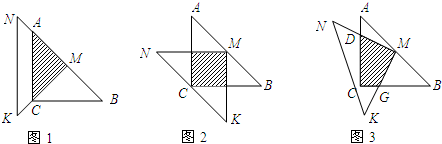
��1����ͼ1�������dzߵ��ص�����Ϊ��ACM�����ص����ֵ����Ϊ______���ܳ�Ϊ______��
��2����ͼ1�еġ�MNK�ƶ���M��ʱ����ת45�㣬�õ�ͼ2����ʱ�ص����ֵ����Ϊ______���ܳ�Ϊ______��
��3���������MNK��M��ת����ͬ��ͼ1��ͼ2��ͼ�Σ���ͼ3����������ʱ�ص����ֵ����Ϊ______��
��4����ͼ3����£���AD=1������ص�����ͼ�ε��ܳ���
�⣺��1����AC=BC=4����ACB=90�㣬
��AB= =
=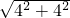 =4
=4 ��
��
��M��AB���е㣬
��AM=2 ��
��
�ߡ�ACM=45�㣬
��AM=MC��
���ص����ֵ������ =4��
=4��
���ܳ�Ϊ��AM+MC+AC=2 +2
+2 +4=4+4
+4=4+4 ��
��
�ʴ�Ϊ��4��4+4 ��
��
��2���ߵ������������Σ�
��߳�Ϊ ��4=2�����Ϊ
��4=2�����Ϊ ��4��4=4��
��4��4=4��
�ܳ�Ϊ2��4=8��
�ʴ�Ϊ��4��8��
��3������M�ֱ���AC��BC�Ĵ���MH��ME������ΪH��E��
��M�ǡ�ABCб��AB���е㣬AC=BC=4��
��MH= BC��
BC��
ME= AC��
AC��
��MH=ME��
�֡ߡ�NMK=��HME=90�㣬
���NMH+��HMK=90�㣬��EMG+��HMK=90�㣬
���HMD=��EMG��
�ڡ�MHD�͡�MEG�У�
��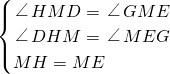 ��
��
���MHD�ա�MEG��ASA����
����Ӱ���ֵ��������������CEMH�������
��������CEMH�������ME•MH= ��4��
��4�� ��4=4��
��4=4��
����Ӱ���ֵ������4��
�ʴ�Ϊ��4��
��4����ͼ��ʾ��
����M��ME��BC�ڵ�E��MH��AC�ڵ�H��
���ı���MECH�Ǿ��Σ�
��MH=CE��
�ߡ�A=45�㣬
���AMH=45�㣬
��AH=MH��
��AH=CE��
��Rt��DHM��Rt��GEM��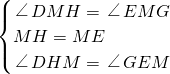 ��
��
��Rt��DHM��Rt��GEM��
��GE=DH��
��AH-DH=CE-GE��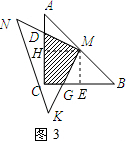
��CG=AD��
��AD=1��
��DH=1��
��DM= =
=
���ı���DMGC���ܳ�Ϊ��
CE+CD+DM+ME
=AD+CD+2DM=4+2 ��
��
��������1������AC=BC=4����ACB=90�㣬�ó�AB��ֵ���ٸ���M��AB���е㣬�ó�AM=MC������ص����ֵ�������ٸ���AM��MC��AC��ֵ��������ܳ���
��2�����ص������������Σ��߳�Ϊ AC�����Ϊ
AC�����Ϊ AC2���ܳ�Ϊ2AC��
AC2���ܳ�Ϊ2AC��
��3������M�ֱ���AC��BC�Ĵ���MH��ME������ΪH��E�����Rt��MHD��Rt��MEG������Ӱ���ֵ��������������CEMH�������
��4���ȹ���M��ME��BC�ڵ�E��MH��AC�ڵ�H�����ݡ�DMH=��EMH��MH=ME���ó�Rt��DHM��Rt��EMG���Ӷ��ó�HD=GE��CE=AD��������AD��DF��ֵ�����DM= �����ɵó��𰸣�
�����ɵó��𰸣�
���������⿼���˵���ֱ�������Σ����õ���ֱ�������ε����ʣ�����ֱ�������ε������ʽ�������ε������ʽ��ȫ�������ε��ж���������⣮
��AB=
 =
=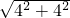 =4
=4 ��
����M��AB���е㣬
��AM=2
 ��
���ߡ�ACM=45�㣬
��AM=MC��
���ص����ֵ������
 =4��
=4�����ܳ�Ϊ��AM+MC+AC=2
 +2
+2 +4=4+4
+4=4+4 ��
���ʴ�Ϊ��4��4+4
 ��
����2���ߵ������������Σ�
��߳�Ϊ
 ��4=2�����Ϊ
��4=2�����Ϊ ��4��4=4��
��4��4=4���ܳ�Ϊ2��4=8��
�ʴ�Ϊ��4��8��
��3������M�ֱ���AC��BC�Ĵ���MH��ME������ΪH��E��
��M�ǡ�ABCб��AB���е㣬AC=BC=4��
��MH=
 BC��
BC��ME=
 AC��
AC����MH=ME��
�֡ߡ�NMK=��HME=90�㣬
���NMH+��HMK=90�㣬��EMG+��HMK=90�㣬
���HMD=��EMG��
�ڡ�MHD�͡�MEG�У�
��
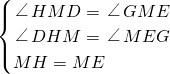 ��
�����MHD�ա�MEG��ASA����
����Ӱ���ֵ��������������CEMH�������
��������CEMH�������ME•MH=
 ��4��
��4�� ��4=4��
��4=4������Ӱ���ֵ������4��
�ʴ�Ϊ��4��
��4����ͼ��ʾ��
����M��ME��BC�ڵ�E��MH��AC�ڵ�H��
���ı���MECH�Ǿ��Σ�
��MH=CE��
�ߡ�A=45�㣬
���AMH=45�㣬
��AH=MH��
��AH=CE��
��Rt��DHM��Rt��GEM��
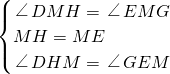 ��
����Rt��DHM��Rt��GEM��
��GE=DH��
��AH-DH=CE-GE��

��CG=AD��
��AD=1��
��DH=1��
��DM=
 =
=
���ı���DMGC���ܳ�Ϊ��
CE+CD+DM+ME
=AD+CD+2DM=4+2
 ��
����������1������AC=BC=4����ACB=90�㣬�ó�AB��ֵ���ٸ���M��AB���е㣬�ó�AM=MC������ص����ֵ�������ٸ���AM��MC��AC��ֵ��������ܳ���
��2�����ص������������Σ��߳�Ϊ
 AC�����Ϊ
AC�����Ϊ AC2���ܳ�Ϊ2AC��
AC2���ܳ�Ϊ2AC����3������M�ֱ���AC��BC�Ĵ���MH��ME������ΪH��E�����Rt��MHD��Rt��MEG������Ӱ���ֵ��������������CEMH�������
��4���ȹ���M��ME��BC�ڵ�E��MH��AC�ڵ�H�����ݡ�DMH=��EMH��MH=ME���ó�Rt��DHM��Rt��EMG���Ӷ��ó�HD=GE��CE=AD��������AD��DF��ֵ�����DM=
 �����ɵó��𰸣�
�����ɵó��𰸣����������⿼���˵���ֱ�������Σ����õ���ֱ�������ε����ʣ�����ֱ�������ε������ʽ�������ε������ʽ��ȫ�������ε��ж���������⣮

��ϰ��ϵ�д�
�����Ŀ
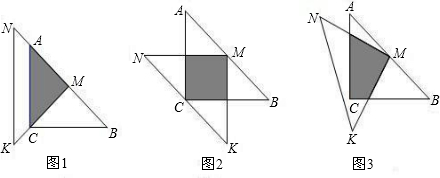
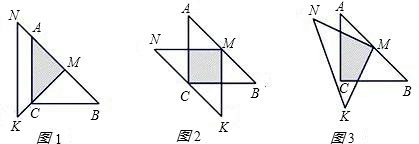
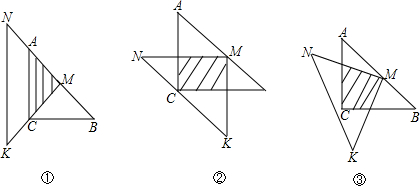
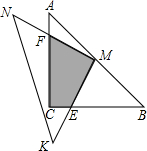 ��ͼ��ʾ��һλͬѧ��������45������dzߡ�MNK����ACB����һ��̽���������MNK��ֱ�Ƕ���M���ڡ�ABC��б��AB���е㴦����AC=BC=a��
��ͼ��ʾ��һλͬѧ��������45������dzߡ�MNK����ACB����һ��̽���������MNK��ֱ�Ƕ���M���ڡ�ABC��б��AB���е㴦����AC=BC=a��