题目内容
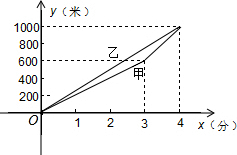 (2013•石景山区二模)甲、乙两位同学进行长跑训练,两人距出发点的路程y(米)与跑步时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答问题:
(2013•石景山区二模)甲、乙两位同学进行长跑训练,两人距出发点的路程y(米)与跑步时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答问题:(1)他们在进行
1000
1000
米的长跑训练;(2)在3<x<4的时段内,速度较快的人是
甲
甲
;(3)当x=
3分
3分
时,两人相距最远,此时两人距离是多少米?(写出解答过程)分析:(1)根据图象信息可知,他们在进行1000米的长跑训练;
(2)在3<x<4的时段内,速度较快的人是甲;
(3)甲、乙两位同学从同一地点同时出发,在0<x≤3的时段内,由于甲的速度小于乙的速度,所以乙超过甲,并且两人相距越来越远;在3<x<4的时段内,由于甲的速度大于乙的速度,所以甲在后面追赶乙,两人相距越来越近;在x=4时,甲追上乙,两人同时到达终点,故当x=3时,两人相距最远.分别求出x=3时,两人距出发点的路程y,再用y乙减去y甲即可.
(2)在3<x<4的时段内,速度较快的人是甲;
(3)甲、乙两位同学从同一地点同时出发,在0<x≤3的时段内,由于甲的速度小于乙的速度,所以乙超过甲,并且两人相距越来越远;在3<x<4的时段内,由于甲的速度大于乙的速度,所以甲在后面追赶乙,两人相距越来越近;在x=4时,甲追上乙,两人同时到达终点,故当x=3时,两人相距最远.分别求出x=3时,两人距出发点的路程y,再用y乙减去y甲即可.
解答:解:(1)根据图象信息可知他们在进行1000米的长跑训练;
(2)根据图象信息可知在3<x<4的时段内,速度较快的人是甲;
(3)设乙距出发点的路程y(米)与跑步时间x(分)之间的函数解析式为y乙=k1x,
将(4,1000)代入,得4k1=1000,解得k1=250,
所以y乙=250x.
在0<x≤3的时段内,设甲距出发点的路程y(米)与跑步时间x(分)之间的函数解析式为y甲=k2x,
将(3,600)代入,得3k2=600,解得k2=200,
所以y2=200x.
当x=3分时,两人相距最远,此时两人距离是:250x-200x=50x=50×3=150米.
答:当x=3分时,两人相距最远,此时两人距离是150米.
故答案为1000;甲;150米.
(2)根据图象信息可知在3<x<4的时段内,速度较快的人是甲;
(3)设乙距出发点的路程y(米)与跑步时间x(分)之间的函数解析式为y乙=k1x,
将(4,1000)代入,得4k1=1000,解得k1=250,
所以y乙=250x.
在0<x≤3的时段内,设甲距出发点的路程y(米)与跑步时间x(分)之间的函数解析式为y甲=k2x,
将(3,600)代入,得3k2=600,解得k2=200,
所以y2=200x.
当x=3分时,两人相距最远,此时两人距离是:250x-200x=50x=50×3=150米.
答:当x=3分时,两人相距最远,此时两人距离是150米.
故答案为1000;甲;150米.
点评:本题考查了一次函数的应用,解决此类题目的关键是从已知函数图象中获取信息,运用待定系数法求出函数解析式,并解答相应的问题.

练习册系列答案
相关题目
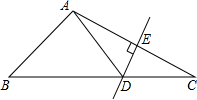 (2013•石景山区二模)如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( )
(2013•石景山区二模)如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为( ) (2013•石景山区二模)如图,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( )
(2013•石景山区二模)如图,AB是⊙O的直径,C是⊙O上的一点,若AC=8,AB=10,OD⊥BC于点D,则BD的长为( )