题目内容
在m（a-x）（x-b）-mn（a-x）（b-x）中，公因式是
- A.m
- B.m（a-x）
- C.m（a-x）（b-x）
- D.（a-x）（b-x）
C
分析：首先把式子进行变形，可变为m（a-x）（x-b）+mn（a-x）（x-b），进而可得到公因式m（a-x）（b-x）．
解答：m（a-x）（x-b）-mn（a-x）（b-x），
=m（a-x）（x-b）+mn（a-x）（x-b），
=m（a-x）（x-b）（1+n），
故选：C．
点评：此题主要考查了找公因式的方法，找公因式的要点是：（1）公因式的系数是多项式各项系数的最大公约数；（2）字母取各项都含有的相同字母；（3）相同字母的指数取次数最低的．
分析：首先把式子进行变形，可变为m（a-x）（x-b）+mn（a-x）（x-b），进而可得到公因式m（a-x）（b-x）．
解答：m（a-x）（x-b）-mn（a-x）（b-x），
=m（a-x）（x-b）+mn（a-x）（x-b），
=m（a-x）（x-b）（1+n），
故选：C．
点评：此题主要考查了找公因式的方法，找公因式的要点是：（1）公因式的系数是多项式各项系数的最大公约数；（2）字母取各项都含有的相同字母；（3）相同字母的指数取次数最低的．
练习册系列答案
相关题目
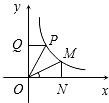设P（a，b），M（c，d）是反比例函数y=
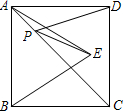如图所示，正方形ABCD的面积为18，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（ ）
20、如图，在△ABC中，点D，E分别是AB，AC边的中点，若把△ADE绕着点E顺时针旋转180°得到△CFE．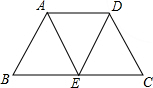
在等腰梯形ABCD中，AD∥BC，E是BC的中点，连接AE，DE，AE与DE相等吗？
