题目内容
(满分8分)如图,已知直线AB与 轴交于点C,与双曲线
轴交于点C,与双曲线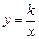 交于A(3,
交于A(3,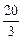 )、B(-5,
)、B(-5,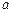 )两点.AD⊥
)两点.AD⊥ 轴于点D,BE∥
轴于点D,BE∥ 轴且与
轴且与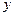 轴交于点E.
轴交于点E.
(1)求点B的坐标及直线AB的解析式;
(2)判断四边形CBED的形状,并说明理由.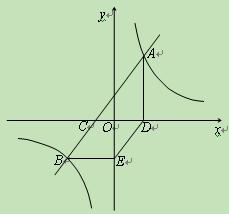
解:(1)∵双曲线 过A(3,
过A(3,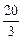 ),∴
),∴ .把B(-5,
.把B(-5,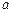 )代入
)代入 ,
,
得 . ∴点B的坐标是(-5,-4). ……………………………… 2分
. ∴点B的坐标是(-5,-4). ……………………………… 2分
设直线AB的解析式为 ,
,
将 A(3,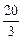 )、B(-5,-4)代入得,
)、B(-5,-4)代入得, , 解得:
, 解得: .
.
∴直线AB的解析式为: .………………………………… 4分
.………………………………… 4分
(2)四边形CBED是菱形.理由如下: ………………………………… 5分
点D的坐标是(3,0),点C的坐标是(-2,0).
∵ BE∥ 轴, ∴点E的坐标是(0,-4).
轴, ∴点E的坐标是(0,-4).
而CD =5, BE=5,且BE∥CD.
∴四边形CBED是平行四边形.………………………………………… 6分
在Rt△OED中,ED2=OE2+OD2,∴ ED= =5,∴ED=CD.
=5,∴ED=CD.
∴□CBED是菱形.……………………………………………………… 8分
解析

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
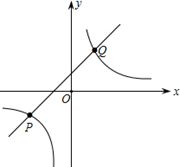
 +b的图象与反比例函数
+b的图象与反比例函数

 弦,OB=2,∠B=30°,
弦,OB=2,∠B=30°,
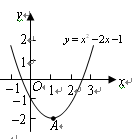
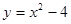 ,将
,将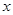 轴下方的图象沿
轴下方的图象沿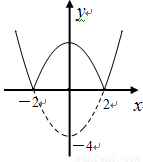
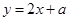 的图像与新图象公共点的个数情况.
的图像与新图象公共点的个数情况.