题目内容
如图,已知抛物线 与y轴相交于C,与x轴相交于A、B,点A的坐
与y轴相交于C,与x轴相交于A、B,点A的坐 标为(2,0),点C的坐标为(0,-1).
标为(2,0),点C的坐标为(0,-1).
(1)求抛物线的解析式;
(2)设点P为此抛物线的顶点,求∠OAP的余弦;
(3)设点M为此抛物线上的一点,且MC⊥AC,求点M的坐标?
解:(1)∵抛物线 过A(2,0),C(0,-1)
过A(2,0),C(0,-1)
∴ ,
,
解得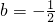 ,
,
∴抛物线的解析式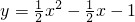
(2)∵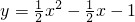 =
=
∴顶点
∴ ,
,
∴ ;
;

(3)设M点的坐标为 ,
,
过M点作MD⊥y轴于D,则△CDM∽△AOC
∴
∴ ,
,
∴x=-3
∴ ,
,
∴点M的坐标为(-3,5).
分析:(1)将A(2,0),C(0,-1)两点坐标代入抛物线 ,即可求得抛物线的解析式;
,即可求得抛物线的解析式;
(2)先求出P点坐标,根据cos∠OAP= 即可求出∠OAP的余弦;
即可求出∠OAP的余弦;
(3)过M点作MD⊥y轴于D,根据三角形相似的性质解得x值,便可求出点M的坐标.
点评:本题是二次函数的综合题,其中涉及到的知识点有抛物线的公式的求法和三角形的相似等知识点,是各地中考的热点和难点,解题时注意数形结合数学思想的运用,同学们要加强训练,属于中档题.
 过A(2,0),C(0,-1)
过A(2,0),C(0,-1)∴
 ,
,解得
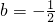 ,
,∴抛物线的解析式
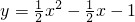
(2)∵
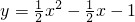 =
=
∴顶点

∴
 ,
,∴
 ;
; 
(3)设M点的坐标为
 ,
, 过M点作MD⊥y轴于D,则△CDM∽△AOC
∴

∴
 ,
,∴x=-3
∴
 ,
,∴点M的坐标为(-3,5).
分析:(1)将A(2,0),C(0,-1)两点坐标代入抛物线
 ,即可求得抛物线的解析式;
,即可求得抛物线的解析式;(2)先求出P点坐标,根据cos∠OAP=
 即可求出∠OAP的余弦;
即可求出∠OAP的余弦;(3)过M点作MD⊥y轴于D,根据三角形相似的性质解得x值,便可求出点M的坐标.
点评:本题是二次函数的综合题,其中涉及到的知识点有抛物线的公式的求法和三角形的相似等知识点,是各地中考的热点和难点,解题时注意数形结合数学思想的运用,同学们要加强训练,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
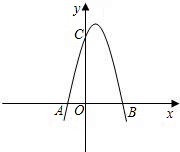 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).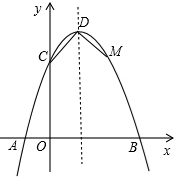 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1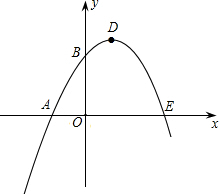 函数的最大值是4.
函数的最大值是4. (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )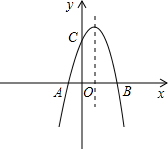 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).