题目内容
 如图,腰长为6的等腰直角三角形ABC绕点A顺时针旋转15°,则图中阴影部分的面积为________.
如图,腰长为6的等腰直角三角形ABC绕点A顺时针旋转15°,则图中阴影部分的面积为________.

分析:根据等腰直角三角形的性质得∠BAC=45°,由于等腰直角三角形ABC绕点A顺时针旋转15°,根据旋转的性质得∠BAB′=15°,∠B′=∠B,AB′=AB=6,则∠B′AC=∠BAC-∠BAB′=30°,利用
含30度的直角三角形三边的关系得到B′D=
 AB′=2
AB′=2 ,然后根据三角形面积公式计算图中阴影部分的面积.
,然后根据三角形面积公式计算图中阴影部分的面积.解答:如图,
∵△ABC为腰长为6的等腰直角三角形,

∴∠BAC=45°,
∵等腰直角三角形ABC绕点A顺时针旋转15°,
∴∠BAB′=15°,∠B′=∠B,AB′=AB=6,
∴∠B′AC=∠BAC-∠BAB′=30°,
在Rt△AB′D中,∠B′AD=30°,AB′=6,
∴B′D=
 AB′=2
AB′=2 ,
,∴图中阴影部分的面积=
 AB′•B′D=
AB′•B′D= ×6×2
×6×2 =6
=6 .
.故答案为6
 .
.点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等腰直角三角形的性质以及含30度的直角三角形三边的关系.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
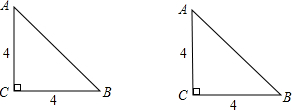
 在平面直角坐标系中,将一块腰长为
在平面直角坐标系中,将一块腰长为 如图,腰长为6的等腰直角三角形ABC绕点A顺时针旋转15°,则图中阴影部分的面积为
如图,腰长为6的等腰直角三角形ABC绕点A顺时针旋转15°,则图中阴影部分的面积为