题目内容
在Rt△ABC中,已知斜边长为c,两直角边长为a,b.求证:
+
=
.
|
|
| 2c |
| b |
分析:所证等式左边平方,通分并利用同分母分式的加法法则计算,得到结果为右边的平方,得证.
解答:解:∵在Rt△ABC中,已知斜边长为c,两直角边长为a,b,
∴c2=a2+b2,
左边2=
+
+2=
=
=
,
右边2=
,
∴左边=右边,即原式成立.
∴c2=a2+b2,
左边2=
| c+a |
| c-a |
| c-a |
| c+a |
| (c+a)2+(c-a)2+2(c+a)(c-a) |
| (c+a)(c-a) |
| 4c2 |
| c2-a2 |
| 4c2 |
| b2 |
右边2=
| 4c2 |
| b2 |
∴左边=右边,即原式成立.
点评:此题考查了勾股定理,以及二次根式的化简求值,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在Rt△ABC中,已知∠C=90°,∠A=30°,BD是∠B的平分线,AC=18,则BD的值为( )
A、3
| ||
| B、9 | ||
| C、12 | ||
| D、6 |
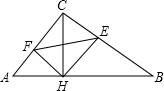 如图,在Rt△ABC中,已知∠ACB=90°,且CH⊥AB,HE⊥BC,HF⊥AC.
如图,在Rt△ABC中,已知∠ACB=90°,且CH⊥AB,HE⊥BC,HF⊥AC.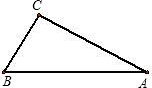 如图,在Rt△ABC中,已知∠BCA=90°,∠BAC=30°,AB=6cm.把△ABC以点B为中心逆时针旋转,使点C旋转到AB边的延长线上得到Rt△A1BC1.
如图,在Rt△ABC中,已知∠BCA=90°,∠BAC=30°,AB=6cm.把△ABC以点B为中心逆时针旋转,使点C旋转到AB边的延长线上得到Rt△A1BC1. 如图,在Rt△ABC中,已知∠ABC=90°,BC=6,以AB为直径作⊙O,连接OC,过点C作⊙O的切线CD,D为切点,若sin∠OCD=
如图,在Rt△ABC中,已知∠ABC=90°,BC=6,以AB为直径作⊙O,连接OC,过点C作⊙O的切线CD,D为切点,若sin∠OCD= 如图,在Rt△ABC中,已知tanB=2,则sinA的值是( )
如图,在Rt△ABC中,已知tanB=2,则sinA的值是( )