题目内容
如图,在![]() 中,∠
中,∠![]()
![]() °,
°,![]() ,
, ![]() 的面积为
的面积为![]() ,点
,点![]() 为
为![]() 边上的任意一点(
边上的任意一点(![]() 不与
不与![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 于点
于点![]() .设
.设![]() 以
以![]() 为折线将△
为折线将△![]() 翻折,所得的
翻折,所得的![]() 与梯形
与梯形![]() 重叠部分的面积记为y.
重叠部分的面积记为y.
(1).用x表示∆ADE的面积;
(2).求出![]()
![]() ≤
≤![]() 时y与x的函数关系式;
时y与x的函数关系式;
(3).求出![]()
![]()
![]() 时y与x的函数关系式;
时y与x的函数关系式;
(4).当![]() 取何值时,
取何值时,![]() 的值最大?最大值是多少?
的值最大?最大值是多少?
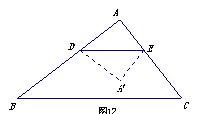
解:(1)∵ DE∥BC ∴∠ADE=∠B,∠AED=∠C
∴△ADE∽△ABC ∴![]()
![]()
即![]()
(2)∵BC=10 ∴BC边所对的三角形的中位线长为5
∴当0![]() 时
时 ![]()
(3)![]() 10时,点A'落在三角形的外部,其重叠部分为梯形
10时,点A'落在三角形的外部,其重叠部分为梯形
∵S△A'DE=S△ADE=![]()
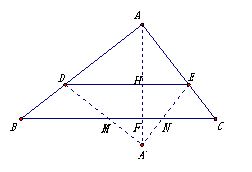 ∴DE边上的高AH=AH'=
∴DE边上的高AH=AH'=![]()
由已知求得AF=5
∴A'F=AA'-AF=x-5
由△A'MN∽△A'DE知
![]()
![]()
∴![]()
(4)在函数![]() 中
中
∵0x≤5
∴当x=5时y最大为:![]()
在函数![]()
![]() 中
中
当![]() 时y最大为:
时y最大为:![]()
∵![]()
![]()
∴当![]() 时,y最大为:
时,y最大为:![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, 是
是 边上的高,
边上的高, 是
是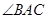 平分线。求
平分线。求 的度数。
的度数。
 中,
中, ,
, 平分
平分 交
交 于
于 ,点
,点 在
在 上,以
上,以 为半径的圆,交
为半径的圆,交 ,交
,交 于
于 ,且点
,且点 ,切⊙
,切⊙


 ,求⊙
,求⊙ 中,
中, D是BC上的点,
D是BC上的点,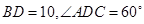 .求AC(
.求AC(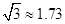 ,结果保留整数).
,结果保留整数).
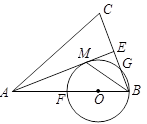
 中,
中, ,点
,点 在
在 上,以
上,以 长为半径的圆与
长为半径的圆与 分别交于点
分别交于点 ,且
,且 .
. 与
与 的位置关系,并证明你的结论;
的位置关系,并证明你的结论; ,
, ,求
,求 的值.
的值.