题目内容
 下图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).
下图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).(1)求出图象与x轴的交点A,B的坐标;
(2)在二次函数的图象上是否存在点P,使S△PAB=
| 5 | 4 |
(3)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b(b<1)与此图象有两个公共点时,b的取值范围.
分析:(1)由顶点坐标确定m、k的值,再令y=0求得图象与x轴的交点坐标;
(2)设存在这样的P点,由于底边相同,求出△PAB的高|y|,将y求出代入二次函数表达式求得P点坐标;
(3)画出翻转后新的函数图象,由直线y=x+b,b<1确定出直线移动的范围,求出b的取值范围.
(2)设存在这样的P点,由于底边相同,求出△PAB的高|y|,将y求出代入二次函数表达式求得P点坐标;
(3)画出翻转后新的函数图象,由直线y=x+b,b<1确定出直线移动的范围,求出b的取值范围.
解答: 解:(1)因为M(1,-4)是二次函数y=(x+m)2+k的顶点坐标,
解:(1)因为M(1,-4)是二次函数y=(x+m)2+k的顶点坐标,
所以y=(x-1)2-4=x2-2x-3,
令x2-2x-3=0,
解之得x1=-1,x2=3.
∴A,B两点的坐标分别为A(-1,0),B(3,0);(4分)
(2)在二次函数的图象上存在点P,使S△PAB=
S△MAB,
设P(x,y),
则S△PAB=
|AB|×|y|=2|y|,
又∵S△MAB=
|AB|×|-4|=8,
∴2|y|=
×8,即y=±5.
∵二次函数的最小值为-4,
∴y=5.
当y=5时,x=-2或x=4.
故P点坐标为(-2,5)或(4,5);
(3)如图,当直线y=x+b经过A(-1,0)时-1+b=0,可得b=1,又因为b<1,
故可知y=x+b在y=x+1的下方,
当直线y=x+b经过点B(3,0)时,3+b=0,则b=-3,
由图可知符合题意的b的取值范围为-3<b<1时,直线y=x+b(b<1)与此图象有两个公共点.
 解:(1)因为M(1,-4)是二次函数y=(x+m)2+k的顶点坐标,
解:(1)因为M(1,-4)是二次函数y=(x+m)2+k的顶点坐标,所以y=(x-1)2-4=x2-2x-3,
令x2-2x-3=0,
解之得x1=-1,x2=3.
∴A,B两点的坐标分别为A(-1,0),B(3,0);(4分)
(2)在二次函数的图象上存在点P,使S△PAB=
| 5 |
| 4 |
设P(x,y),
则S△PAB=
| 1 |
| 2 |
又∵S△MAB=
| 1 |
| 2 |
∴2|y|=
| 5 |
| 4 |
∵二次函数的最小值为-4,
∴y=5.
当y=5时,x=-2或x=4.
故P点坐标为(-2,5)或(4,5);
(3)如图,当直线y=x+b经过A(-1,0)时-1+b=0,可得b=1,又因为b<1,
故可知y=x+b在y=x+1的下方,
当直线y=x+b经过点B(3,0)时,3+b=0,则b=-3,
由图可知符合题意的b的取值范围为-3<b<1时,直线y=x+b(b<1)与此图象有两个公共点.
点评:本题考查了由函数图象确定坐标,以及给出面积关系求点的坐标和直线与图象的交点问题,综合体现了数形结合的思想.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 的大致图象,那么一次函数
的大致图象,那么一次函数 的图象不经过
的图象不经过
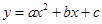 的图像,与
的图像,与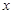 轴交于
轴交于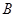 ,
,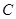 两点,与
两点,与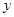 轴交于
轴交于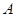 点.
点.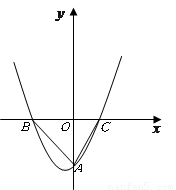
 ,
,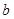 ,
,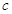 的符号,并说明理由;
的符号,并说明理由;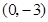 ,
,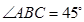 ,
,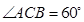 ,求这个二次函数的函数表达式.
,求这个二次函数的函数表达式. 的大致图象,那么一次函数
的大致图象,那么一次函数 的图象不经过
的图象不经过