题目内容
【题目】如图,在正方形ABCD中,AB=BC=CD=AD,∠BAD=∠B=∠C=∠D=90°,点E、F分别在正方形ABCD的边DC、BC上,AG⊥EF且 AG=AB,垂足为G,则: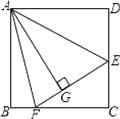
(1)△ABF与△ AGF全等吗?说明理由;
(2)求∠EAF的度数;
(3)若AG=4,△AEF的面积是6,求△CEF的面积.
【答案】
(1)解:△ABF与△ AGF全等,理由如下:
在Rt![]() ABF和Rt
ABF和Rt![]() AGF中,
AGF中,![]() ,
,
∴△ABF![]() △ AGF.
△ AGF.
(2)解:∵△ABF![]() △ AGF,
△ AGF,
∴![]() BAF=
BAF=![]() GAF,
GAF,
同理易得:△AGE![]() △ ADE,有
△ ADE,有![]() GAE=
GAE=![]() DAE,
DAE,
即![]() EAF=
EAF=![]() EAD+
EAD+![]() FAG=
FAG=![]()
![]() BAD=45
BAD=45![]() .
.
(3)解:∵S![]() AEF=
AEF=![]()
![]() EF
EF![]() AG,AG=4,
AG,AG=4,
∴6=![]()
![]() EF
EF![]() AG,
AG,
∴EF=3,
∵BF=FG,EG=DE,AG=AB=BC=CD=4,设FC=x,EC=y,则BF=4-x,DE=4-y,
∵BF+DE=FG+EG=EF=3,
∴4-x+4-y=3,
∴x+y=5 ①
在Rt![]() EFC中,∵EF2=EC2+FC2,
EFC中,∵EF2=EC2+FC2,
∴x2+y2=32 ②
①2-②得到,2xy=16,
∴S![]() CEF=
CEF=![]() xy=4.
xy=4.
【解析】(1)根据HL可得出△ABF![]() △ AGF;(2)只要证明
△ AGF;(2)只要证明![]() BAF=
BAF=![]() GAF,
GAF,![]() GAE=
GAE=![]() DAE,即可求出
DAE,即可求出![]() EAF=45
EAF=45![]() ;(3)设FC=x,EC=y,则BF=4-x,DE=4-y,构建方程组,求出xy即可求出△CEF的面积.
;(3)设FC=x,EC=y,则BF=4-x,DE=4-y,构建方程组,求出xy即可求出△CEF的面积.
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

【题目】甲,乙,丙,丁四名跳高运动员赛前几次选拔赛成绩如表所示,根据表中的信息,如果要从中,选择一名成绩好又发挥稳定的运动员参加比赛,那么应选 .
甲 | 乙 | 丙 | 丁 | |
平均数(cm) | 185 | 180 | 185 | 180 |
方差 | 3.6 | 3.6 | 7.9 | 8.2 |

