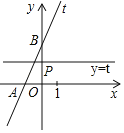题目内容
【题目】如图,抛物线![]() 经过点
经过点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.

(1)求该抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 平行于
平行于![]() 轴,交
轴,交![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,试求出线段
,试求出线段![]() 的最大值,并写出此时点
的最大值,并写出此时点![]() 的坐标;
的坐标;
(3)抛物线上是否存在一点![]() ,使得
,使得![]() ,若存在,请直接写出点
,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)利用待定系数法求解即可;
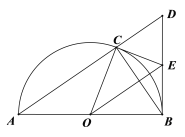
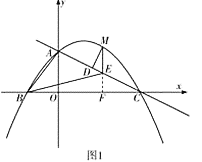
(2)如图1,延长![]() 交
交![]() 轴于点
轴于点![]() ,先利用锐角三角函数的知识得到MD与ME的关系式,把求MD的最大值转化为求ME的最大值,再利用ME=MF-EN得出ME关于m的函数关系式,然后利用二次函数的性质即可求出ME的最大值,问题即得解决;
,先利用锐角三角函数的知识得到MD与ME的关系式,把求MD的最大值转化为求ME的最大值,再利用ME=MF-EN得出ME关于m的函数关系式,然后利用二次函数的性质即可求出ME的最大值,问题即得解决;
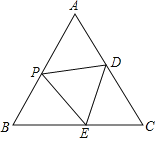
(3)如图2,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,先证明
,先证明![]() 是等腰三角形,得
是等腰三角形,得![]() =
=![]() ∠ABC,当点P在x轴上方时,过点
∠ABC,当点P在x轴上方时,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,则
,则![]() ,于是只要求出直线
,于是只要求出直线![]() 的解析式,再与抛物线的解析式联立组成方程组,解方程组即得符合条件的点P;当点P在x轴下方时,作点
的解析式,再与抛物线的解析式联立组成方程组,解方程组即得符合条件的点P;当点P在x轴下方时,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,作直线
,作直线![]() ,再求直线BH与抛物线的交点即得符合条件的另一个点P.
,再求直线BH与抛物线的交点即得符合条件的另一个点P.
解:(1)将点![]() 和点
和点![]() 代入
代入![]() ,得
,得
![]() .解得
.解得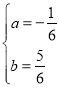
∴抛物线的解析式为![]() .
.
(2)如图1,延长![]() 交
交![]() 轴于点
轴于点![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() .
.
∵A(0,4)![]()
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴当线段![]() 最长时,
最长时,![]() 最长.
最长.
∵点![]() 的横坐标为
的横坐标为![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() .
.
∵点![]() ,
,![]() ,∴直线
,∴直线![]() 的解析式为
的解析式为![]() .
.
∴![]() ,∴
,∴![]() .
.
∴当![]() 时,线段
时,线段![]() 取最大值为
取最大值为![]() .
.
∴相应的MD的最大值为![]() ,此时点M的坐标为
,此时点M的坐标为![]() .
.
(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
理由如下:如图2,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,∵OB=3,OA=4,∴AB=5,
,∵OB=3,OA=4,∴AB=5,
∵![]() =8,∴BC=5=AB,∴
=8,∴BC=5=AB,∴![]() 是等腰三角形,∴
是等腰三角形,∴![]() =
=![]() ∠ABC,
∠ABC,
当点P在x轴上方时,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,则
,则![]() ,∴直线BG与抛物线的交点即为符合条件的点P.
,∴直线BG与抛物线的交点即为符合条件的点P.
此时![]() ,∴点
,∴点![]() ,∴直线
,∴直线![]() 的解析式为
的解析式为![]() .
.
联立方程组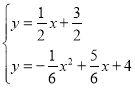 ,解得
,解得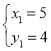 ,
,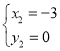 (舍去),
(舍去),
∴点P的坐标为(5,4);
当点P在x轴下方时,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,作直线
,作直线![]() ,则
,则![]() ,可得另一直线
,可得另一直线![]() 的解析式为
的解析式为![]() .
.
解方程组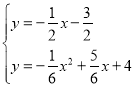 ,得
,得 ,
,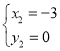 (舍去),
(舍去),
∴点P的坐标为(11,-7);
综上,抛物线上存在一点![]() ,使得
,使得![]() ,且点P的坐标为(5,4)或(11,-7).
,且点P的坐标为(5,4)或(11,-7).