题目内容
无论k取任何实数,对于直线 都会经过一个固定的点
都会经过一个固定的点 ,我们就称直线
,我们就称直线 恒过定点
恒过定点 .
.
(1)无论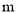 取任何实数,抛物线
取任何实数,抛物线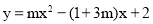 恒过定点
恒过定点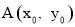 ,直接写出定点A的坐标;
,直接写出定点A的坐标;
(2)已知△ABC的一个顶点是(1)中的定点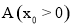 ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线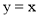 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;
(3)求△ABC内切圆的半径.
(1)(0,2)或(3, );(2)
);(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)将 变形为
变形为 ,只要
,只要 的系数为0,即有无论
的系数为0,即有无论 取任何实数,抛物线
取任何实数,抛物线 恒过定点.
恒过定点.
(2)根据角平分线的轴对称性质,求出点A关于y轴的对称点和关于直线 的对称点的坐标,由该两点在直线BC上,应用待定系数法求解即可.
的对称点的坐标,由该两点在直线BC上,应用待定系数法求解即可.
(3)根据角平分线的性质,y轴和直线 的交点O即为△ABC内切圆的圆心,从而应用面积公式即可求解.
的交点O即为△ABC内切圆的圆心,从而应用面积公式即可求解.
试题解析:(1)∵ 可变形为
可变形为 ,
,
∴当 ,即
,即 或
或 时,无论
时,无论 取任何实数,抛物线
取任何实数,抛物线 恒过定点.
恒过定点.
当 时,
时, ;当
;当 时,
时, ;
;
∴A(0,2)或(3, ).
).
(2)∵△ABC的一个顶点是(1)中的定点 ,
,
∴A(3, ).
).
∵∠B,∠C的角平分线分别是y轴和直线 ,
,
∴点B、点C在点A关于y轴、直线 的对称点所确定的直线上.
的对称点所确定的直线上.
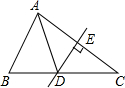
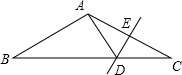
如图,作点A关于y轴的对称点 ,作点A关于直线
,作点A关于直线 的对称点
的对称点 .
.
直线DE与y轴的交点即为点B,与直线 的交点即为点C. 连接AB,AC.
的交点即为点C. 连接AB,AC.
设直线BC的表达式为 .
.
则有 ,解之,得
,解之,得 .
.
所以, .
.

(3) ∵∠B,∠C的角平分线分别是y轴和直线 ,
,
∴y轴和直线 的交点O即为△ABC内切圆的圆心.
的交点O即为△ABC内切圆的圆心.
过点O作OF 于F,则OF即为△ABC内切圆的半径.
于F,则OF即为△ABC内切圆的半径.
设BC与x轴交点为点G,易知 ,
,  .
.
∴ .
.
∵ ,
,
∴ ,即△ABC内切圆的半径为
,即△ABC内切圆的半径为 .
.
考点:1.函数和平面几何综合题;2. 角平分线的性质;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.三角形的内切圆;6.勾股定理;7.三角形面积公式.

 阅读快车系列答案
阅读快车系列答案某校为了更好地开展“阳光体育一小时”活动,围绕着“你最喜欢的体育活动项目是什么(只写一项)?”的问题,对本校学生进行了随机抽样调查,以下是根据得到的相关数据绘制的统计图的一部分.

各年级学生人数统计表
年级 | 七年级 | 八年级 | 九年级 |
学生人数 | 180 | 120 |
|
请根据以上信息解答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)请将图1和图2补充完整;
(3)已知该校七年级学生比九年级学生少20人,请你补全上表,并利用样本数据估计全校学生中最喜欢踢毽子运动的人数约为多少?