题目内容
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB= ,AC=4,BD=10.
,AC=4,BD=10.
问:(1)AC与BD有什么位置关系?说明理由.
(2)四边形ABCD是菱形吗?为什么?
解:(1)AC⊥BD;
∵?ABCD中,OD= BD=5,OA=
BD=5,OA= AC=2
AC=2
又∵△AOD中,OA2+OD2=52+22=29
∴BC2=( )2=29
)2=29
∴△AOD是直角三角形
∴AC⊥BD;
(2)四边形ABCD是菱形;
由?ABCD,得AO=OC,BO=OD
又∵AC⊥BD
∴?ABCD是菱形.
故答案为AC⊥BD、四边形ABCD是菱形.
分析:(1)根据平行四边形对角线互相平分,可以得到OD、OA的长,利用勾股定理逆定理可知△AOD为直角三角形,所以垂直;
(2)由?ABCD,得AO=OC,BO=OD,根据对角线互相垂直的平行四边形是菱形判定.
点评:本题主要考查菱形的判定、平行四边形的性质和勾股定理逆定理.有利于训练学生思维能力.
∵?ABCD中,OD=
 BD=5,OA=
BD=5,OA= AC=2
AC=2又∵△AOD中,OA2+OD2=52+22=29
∴BC2=(
 )2=29
)2=29∴△AOD是直角三角形
∴AC⊥BD;
(2)四边形ABCD是菱形;
由?ABCD,得AO=OC,BO=OD
又∵AC⊥BD
∴?ABCD是菱形.
故答案为AC⊥BD、四边形ABCD是菱形.
分析:(1)根据平行四边形对角线互相平分,可以得到OD、OA的长,利用勾股定理逆定理可知△AOD为直角三角形,所以垂直;
(2)由?ABCD,得AO=OC,BO=OD,根据对角线互相垂直的平行四边形是菱形判定.
点评:本题主要考查菱形的判定、平行四边形的性质和勾股定理逆定理.有利于训练学生思维能力.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=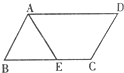 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.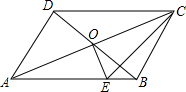 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是