题目内容
(2012•奉贤区三模)如图,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外侧作Rt△ABE和Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q,
(1)若Rt△ABE和Rt△ACF都是等腰三角形,直接写出EP与FQ有怎样的数量关系;
(2)若Rt△ABE和Rt△ACF中满足AB=k AE,AC=k AF时,(1)中的结论还成立吗?若成立,请证明;若不成立,请探究EP与FQ有怎样的数量关系?
(3)若Rt△ABE和Rt△ACF中满足AB=k AE,AC=mAF时,连接EF交射线GA于点D,试探究ED与FD有怎样的数量关系?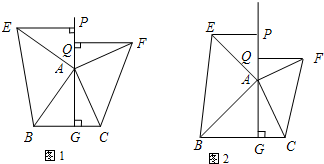
(1)若Rt△ABE和Rt△ACF都是等腰三角形,直接写出EP与FQ有怎样的数量关系;
(2)若Rt△ABE和Rt△ACF中满足AB=k AE,AC=k AF时,(1)中的结论还成立吗?若成立,请证明;若不成立,请探究EP与FQ有怎样的数量关系?
(3)若Rt△ABE和Rt△ACF中满足AB=k AE,AC=mAF时,连接EF交射线GA于点D,试探究ED与FD有怎样的数量关系?

分析:(1)首先根据等腰直角三角形的性质得出AE=AB,∠PEA=∠BAG进而得出△PEA≌△GAB,得出PE=AG,同理可得出QF=AG,即可得出答案;
(2)首先根据对应角∠ABG=∠EAP,∠AGB=∠EPA=90°,得出△ABG∽△EAP,进而得出△ACG∽△FAQ,即可得出
=
求出EP=FQ;
(3)由(2)可知:
=k,
=m,进而得出
=
,再利用平行线性质得出ED与FD的数量关系.
(2)首先根据对应角∠ABG=∠EAP,∠AGB=∠EPA=90°,得出△ABG∽△EAP,进而得出△ACG∽△FAQ,即可得出
| AG |
| EP |
| AG |
| FQ |
(3)由(2)可知:
| AB |
| EA |
| AC |
| FA |
| EP |
| FQ |
| m |
| k |
解答:解:(1)结论:EP=FQ.
理由:∵∠EAB=90°,
∴∠EAP+∠BAG=90°,
∵∠PEA+∠PAE=90°,
∴∠PEA=∠BAG,
在△PEA和△GAB中,
,
∴△PEA≌△GAB(AAS),
∴PE=AG,
∴同理可得出:QF=AG,
∴EP=FQ.
(2)结论:EP=FQ.
理由:∵四边形ABME是矩形,
∴∠BAE=90°,∴∠BAG+∠EAP=90°.
∵AG⊥BC,∴∠BAG+∠ABG=90°,
∴∠ABG=∠EAP.
∵∠AGB=∠EPA=90°,
∴△ABG∽△EAP,
∴
=
.
∵AB=kAE,∴
=k,
同理△ACG∽△FAQ,
∴
=
=k,
∴
=
.
∴EP=FQ.

(3)结论:
=
.
由(2)可知:
∴
=k,
=m
∴
=k,
=m.
∴
=
,
∵EP⊥GA,FQ⊥GA,
∴EP∥FQ.
∴
=
=
.
理由:∵∠EAB=90°,
∴∠EAP+∠BAG=90°,
∵∠PEA+∠PAE=90°,
∴∠PEA=∠BAG,
在△PEA和△GAB中,
|
∴△PEA≌△GAB(AAS),
∴PE=AG,
∴同理可得出:QF=AG,
∴EP=FQ.
(2)结论:EP=FQ.
理由:∵四边形ABME是矩形,
∴∠BAE=90°,∴∠BAG+∠EAP=90°.
∵AG⊥BC,∴∠BAG+∠ABG=90°,
∴∠ABG=∠EAP.
∵∠AGB=∠EPA=90°,
∴△ABG∽△EAP,
∴
| AG |
| EP |
| AB |
| EA |
∵AB=kAE,∴
| AG |
| EP |
同理△ACG∽△FAQ,
∴
| AG |
| FQ |
| AC |
| FA |
∴
| AG |
| EP |
| AG |
| FQ |
∴EP=FQ.

(3)结论:
| ED |
| FD |
| m |
| k |
由(2)可知:
∴
| AB |
| EA |
| AC |
| FA |
∴
| AG |
| EP |
| AG |
| FQ |
∴
| EP |
| FQ |
| m |
| k |
∵EP⊥GA,FQ⊥GA,
∴EP∥FQ.
∴
| ED |
| FD |
| EP |
| FQ |
| m |
| k |
点评:此题主要考查了相似三角形的判定与性质以及全等三角形的判定与性质等知识,根据已知得出△ABG∽△EAP进而得出线段之间关系是解题关键.

练习册系列答案
相关题目