Question

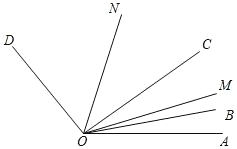
【题目】如图，已知∠AOD=150°，OB、OC、OM、ON 是∠AOD 内的射线，若∠BOC=20°，∠AOB=10°，OM 平分∠AOC，ON 平分∠BOD，当∠BOC 在∠AOD 内绕着点 O以 3°/秒的速度逆时针旋转 t 秒时，当∠AOM：∠DON=3：4 时，则 t=____________．

Answer 1

【答案】

【解析】

由题意得∠AOM=（10°+3t+20°），∠DON=（150°-10°-3t），由此列出方程求解即可．

解：∵射线OB从OA逆时针以3°每秒的旋转t秒，∠BOC=20°，
∴∠AOC=∠AOB+∠COB=3t°+10°+20°=3t°+30°．
∵射线OM平分∠AOC，
∴∠AOM=∠AOC=（3t°+30°）．
∵∠BOD=∠AOD-∠BOA，∠AOD=150°，
∴∠BOD=140°-3t．
∵射线ON平分∠BOD，
∴∠DON=∠BOD=（140°-3t）．
又∵∠AOM：∠DON=3：4，
∴（3t°+30°）：（140°-3t）=3：4，
解得t= ．
故答案是：．