题目内容
袋中有10个球，其中7个是红球，3个是白球，任意取出3个球，这3个球都是红球的概率是
- A.
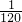
- B.
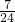
- C.
- D.
B
分析：可以认为分三次取球，第一次有10种可以选择，因而有10种情况，第二次剩余9个球，则第二次有9种情况可以选择，第三次有8种情况，因而可以得到三次取球得到的取法的种数，同理求得三次都是红球的取法，利用概率公式即可求解．
解答：任意取出3个球的情况有：10×9×8=720种；
第一次取到红球的情况有7种，则取第二次，两次都是红球的情况有7×6种，第三次取球，三次都是红球的情况有7×6×5=210种．
则这3个球都是红球的概率是
=．
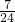故选B．
点评：此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=
．
分析：可以认为分三次取球，第一次有10种可以选择，因而有10种情况，第二次剩余9个球，则第二次有9种情况可以选择，第三次有8种情况，因而可以得到三次取球得到的取法的种数，同理求得三次都是红球的取法，利用概率公式即可求解．
解答：任意取出3个球的情况有：10×9×8=720种；
第一次取到红球的情况有7种，则取第二次，两次都是红球的情况有7×6种，第三次取球，三次都是红球的情况有7×6×5=210种．
则这3个球都是红球的概率是
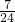=．故选B．
点评：此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=
． 
练习册系列答案
相关题目
设袋中有10个球，其中4个红球，4个白球，2个黑球，每个球除了颜色外都相同，从中随意取出1球，设P1=P（不是红球），P2=P（不是白球），P3=P（不是黑球），则P1、P2、P3的大小关系为（ ）
| A、P1＜P2＜P3 | B、P1＞P2＞P3 | C、P1=P2＜P3 | D、P1=P2＞P3 |